오늘은 어텐션이야
뉴진스 어텐션 아님...
성공적인(?) RNN 발표를 마친 나!
요번 스터디는 못 들어갈 것 같지만
히히 설 날 이슈! 집은 가야지
행복하다 기다리구기다릭던...
그래두 어텐션 열시미 들어보께
ㅎㅇㅌ!
(미친듯이 많이자서 컨디션 굿)
저번시간에 우리는 seq2seq를 언급했었다.
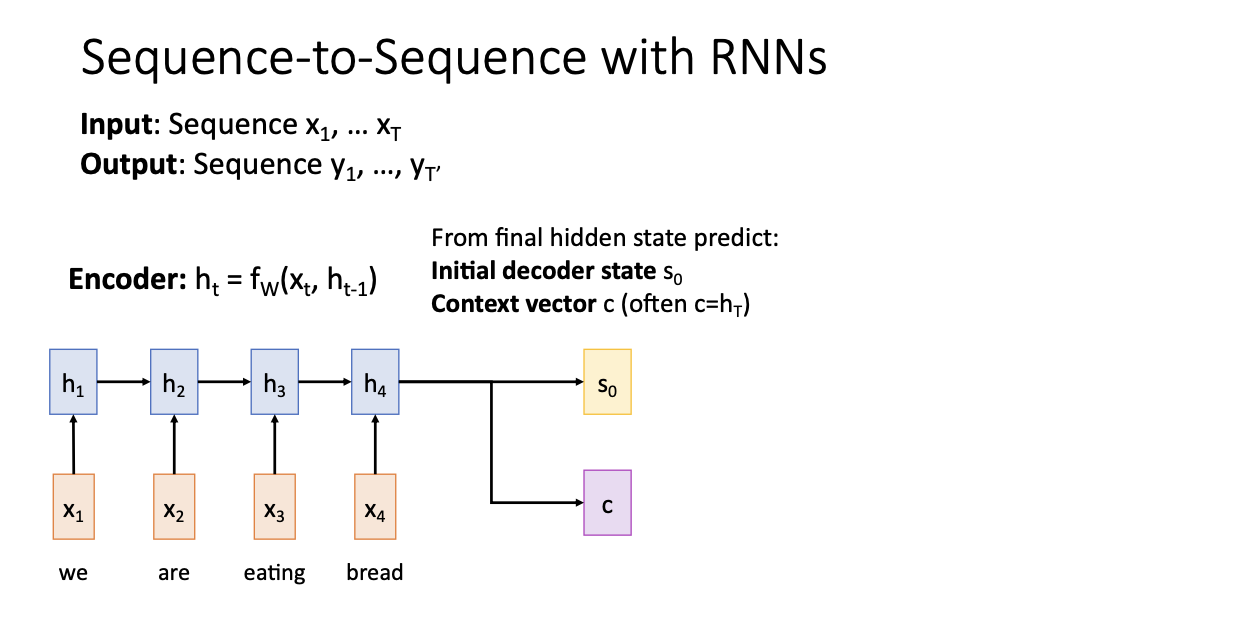
input과 output이 위와 같이 있고 영어를 스페인어로 해석한다고 한다면,
Encoder 과정을 거친 후에는 위와 같이 2가지를 얻을 수 있다.
- initial decoder state s0
- Context vector c : 보통은 ht를 그대로 사용함!
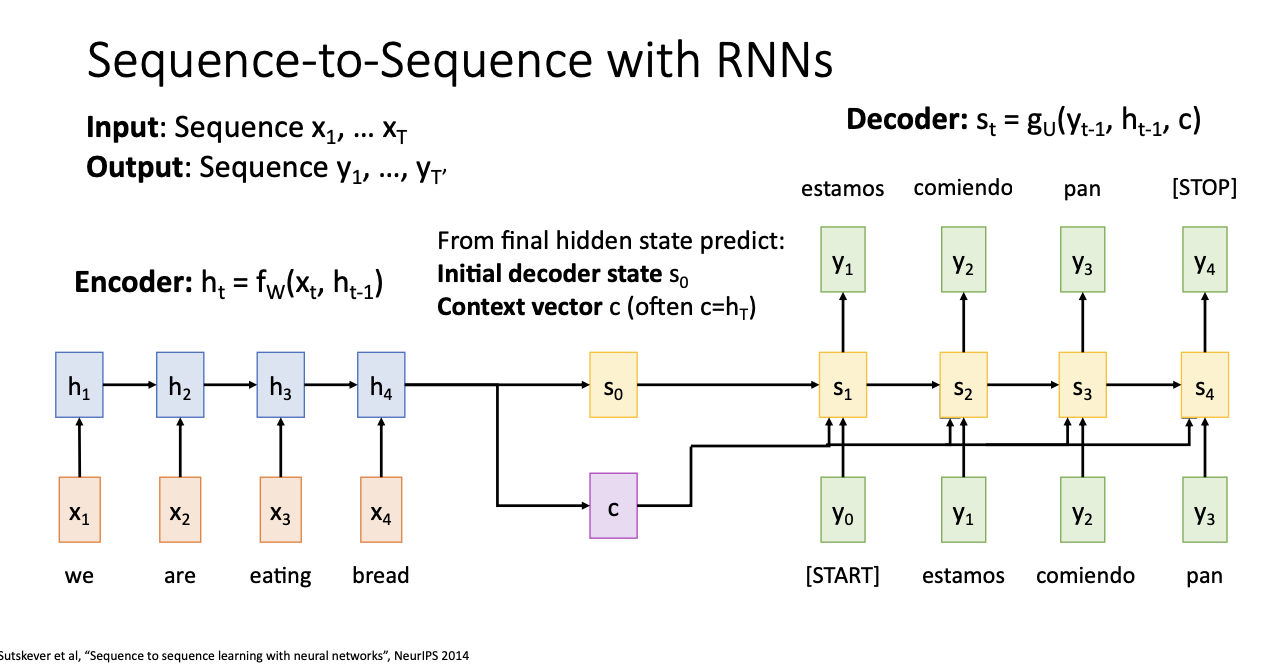
다음은 Decoder 과정이다.
[START]토큰과 [END]라는 토큰을 통해 시작과 끝을 정하는데, s2의 경우만 보면 이전의 hidden state인 s1과 현재 input인 y1, 그리고 Context vector인 c 총 3개를 가지고 만들어지는 것을 볼 수 있다.
하지만 요기서도 문제점이 존재하는데,
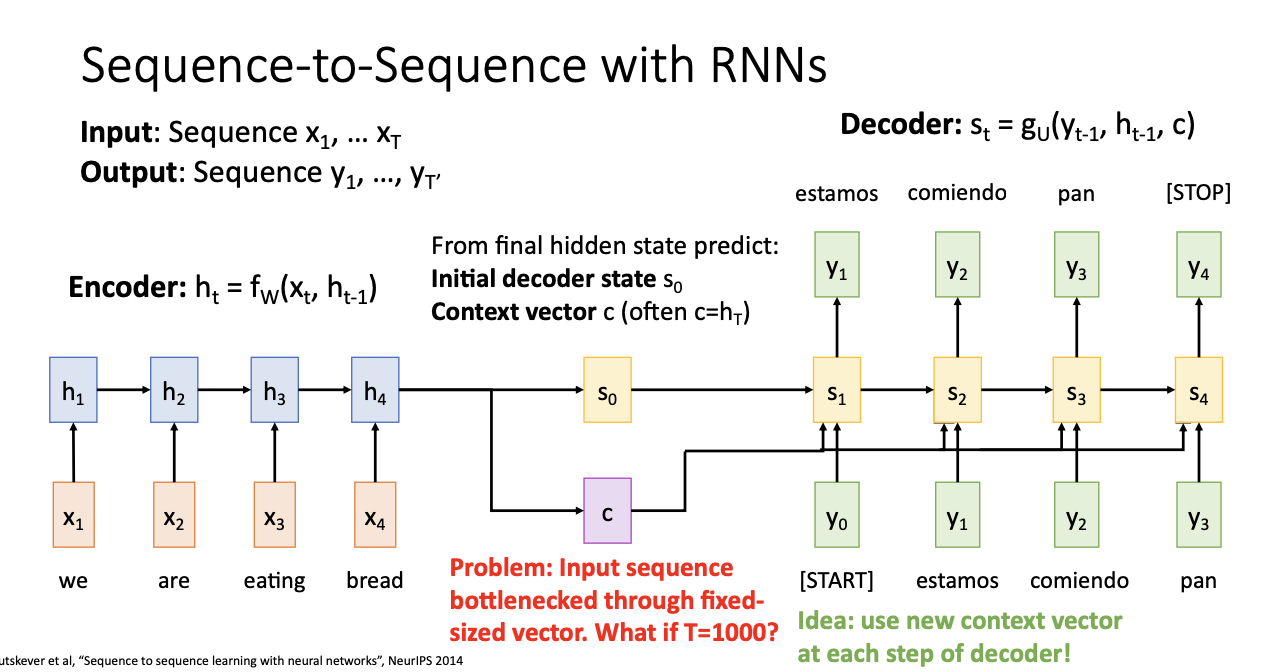
만약 input sequence가 굉장히 길다면? 그러면 T가 매우 길어질테니 모든 정보를 다 모아서 encoding을 진행하고,
하나의 Context vector c에 모든 정보를 담기가 매우 힘겨워질 것이다.
-> 그러면 동일한 c를 계속 적용하지말고, decoder에서 각 step마다 새로운 context vector로 사용하자!
그런 배경에서 등장한 친구가 오늘 배울
Attention
decoder에서 출력 단어를 예측하는 시점시점마다 encoder에서의 전체입력문장을 다시 한 번 참고를 하자!
그런데 여기서 입력 문장 전체가 동일한 비율로 참고되는 것이 아니라 해당 시점에서 예측해야 할 연관이 있는 입력 단어를 조금 더 집중해서 보고 싶은 거야! (그래서 어텐션! 관심!.. 히히 맞나?)

이친구는 첫번째로!
- alignment scores 계산하기!
- fatt라고 하는 함수는 st-1과 hi 2개 사이의 유사도를 측정을 한다.
- 현재 decoder에서 나의 state(s0)와 가장 유사한 hidden state가 있을 것!(h1, h2, h3, h4 중에)
- fatt라고 하는 함수는 st-1과 hi 2개 사이의 유사도를 측정을 한다.

두번째로
- attention weights 구하기!
- 구한 유사도를 softmax를 통해 normalization을 진행
- 일반적으로 et, i 의 범위는 -무한대 ~ 무한대의 범위를 가지는데, 정규화를 통해 0~1사이의 확률값으로 나타나게 됨.

세번째로는
- Context vector를 계산하기!
- 현재 그때그때마다 어디에 초점을 맞춰야 하는지! 어디에 어텐션해야하는지를 정해야하기 때문에..
- 예를 들면 a12가 그 값이 가장 크면! h2가 현재 내가 봐야할 단어!

네번째로
- Context vector를 사용해서 st를 구하기!
- s1을 보면 현재의 우리가 번역하려는 단어 y0와 현재 context, 그림에서 화살표가 빠졌지만 s0을 가지고 만들어 진다.

번역된 예를 보면은 "estamos" 라고 하는 것은 "we are"를 번역한 것이라고 한다.
그렇다면 a11, a12의 조합으로 이루어질 가능성이 크기 때문에 아마 a11, a12가 각각 0.45, a13, a14가 각각 0.05로 다 더하면 1이 되는 확률값이 되었을 것이다.
즉 context vector는 어텐드! 해야하는 input sequence의 상대적인 부분을 나타내는 것이라고 한다.
그래서 이 과정을 반복한다면


s1을 구했다면 s1에 대한 attention scores를 구한 뒤, softmax를 적용시켜 attention weight를 구한 다음 c2를 구하게 된다.
다음 c2를 이용해서 y2와 s2를 구하며 다시 s2를 가지고 이러한 과정을 반복한다.
"comiendo"라는 스페인어는 영어의 "eating"을 뜻한다.
그래서 아마 a21 = a24 = 0.05, a22 = 0.1 이고, a23 = 0.8 로 가장 높은 값을 나타낸다.

그래서! Attention은 decoder과정에서 각 time step에서 다른 context vector를 사용하자! 였다.
더이상 input sequence가 single vector로 나타나지 않고, decoder의 time step마다 어디를 보아야 하는가! 를 말하는 것이다.
실제로 English to French task를 보면

위와 같은 input이 들어갔을 때의 task가 진행되는데 오른쪽의 graph(?)를 통해 attention weight가 시각화 될 것이다.

"The agreement on the"와 "in August 1992"와 같은 경우에는 불어와 1:1로 매핑이 되는 것을 볼 수 있다.

그치만 "European Economic Area"의 경우에는 1:1로 매핑이 되지 않고 단어 개수가 달라지게 된다.
그래서 오른쪽에 초록색 상자를 보면 각각 단어에 대해 attention된 것을 볼 수 있다.

빨간색인 부분도 위와 같이 attention되어 번역이 이루어지고 있다.
따라서 attention은
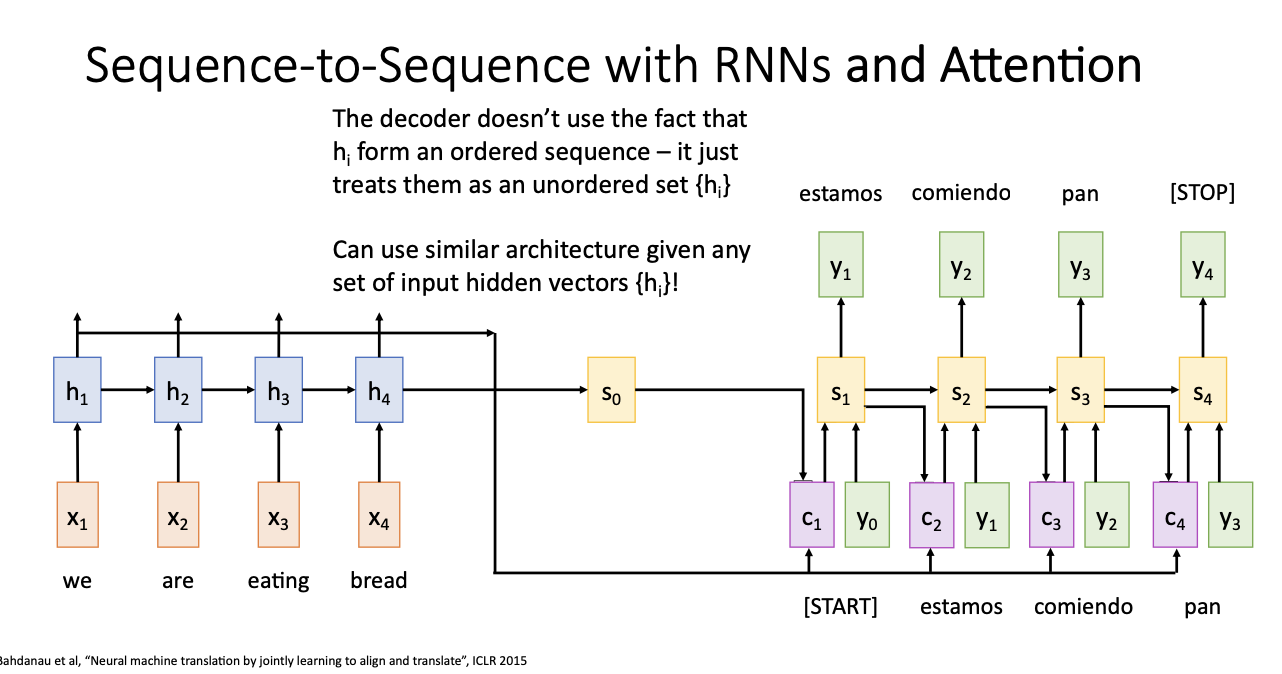
hi가.. hidden state가 순서가 있는 sequence라는 사실을 사용하지 않고, 순서가 없는 집합으로 생각하고 있는 것이다.
그래서 eating bread라는 순서로 들어오지 않아도 그 시간적 순서를 사용하지 않는 것이다. (?)
앞부분은 language에 대해 이야기했다면 이제는 image에 대해서 다루어보자.
앞 포스팅에서 다루었던 RNN에서의 Image Captioning인데 거기에 Attention을 곁들인 ..

CNN을 통해 이미지가 가진 정보를 gird로 뽑은 다음에 위에서 설명했듯
st-1과 통해 hij를 통해 ftt를 통해 alignment score를 계산한다. 각 요소에 대해서 et,i,j를 구할 수 있게 된다.
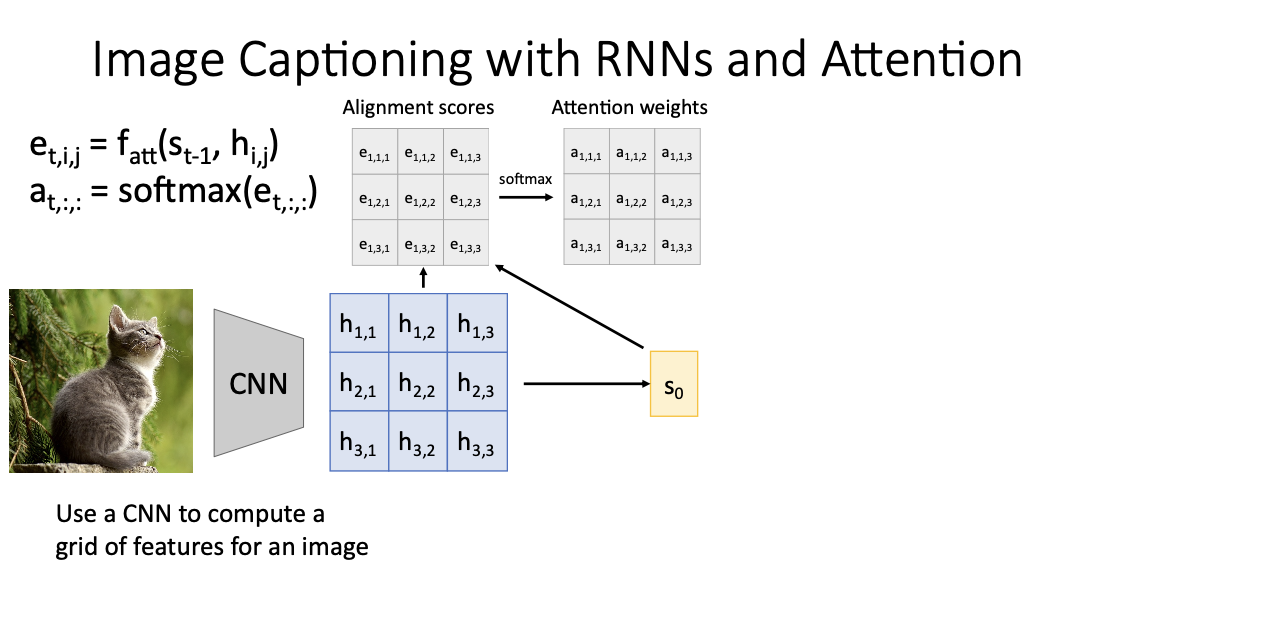
다음 이 alignment score에 softmax를 씌워서 attention weights를 구하게 되고,
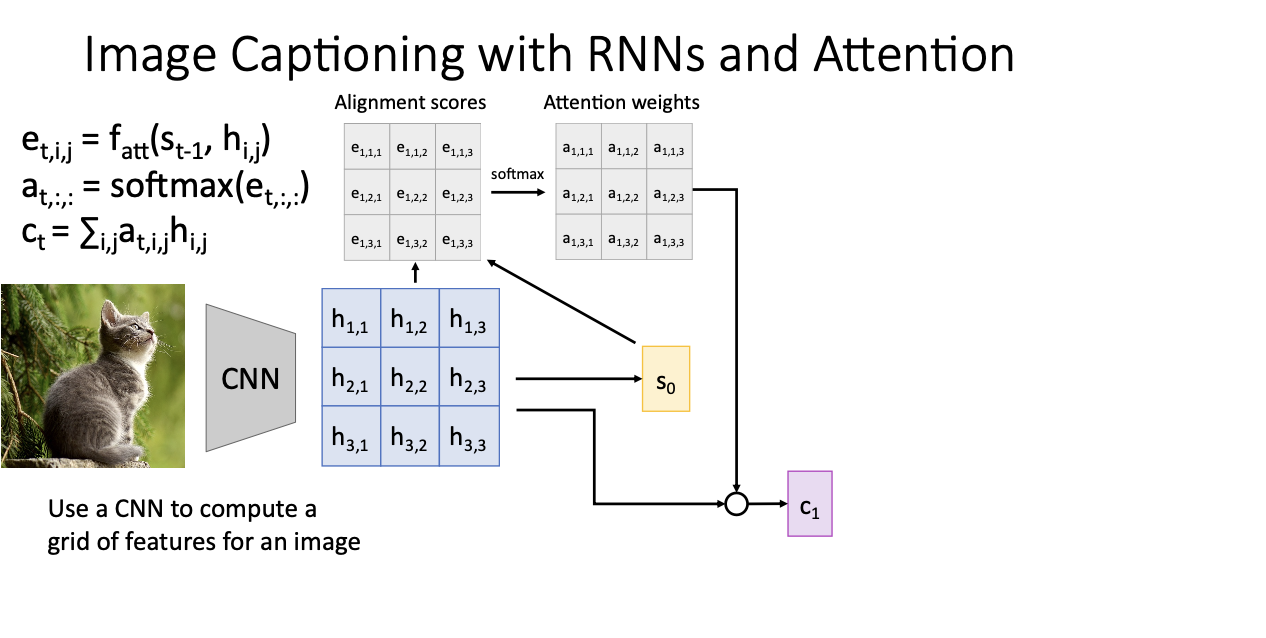
그렇게 구하게된 attention weights과 CNN을 통해서 구한 grid of features의 적절한 합을 통해 c1을 구하게 된다.
여기서 우리는 이제 CNN을 통한 feature grid에서 어떤 부분을 attention해야 하는 것이냐! 를 생각해야한다.
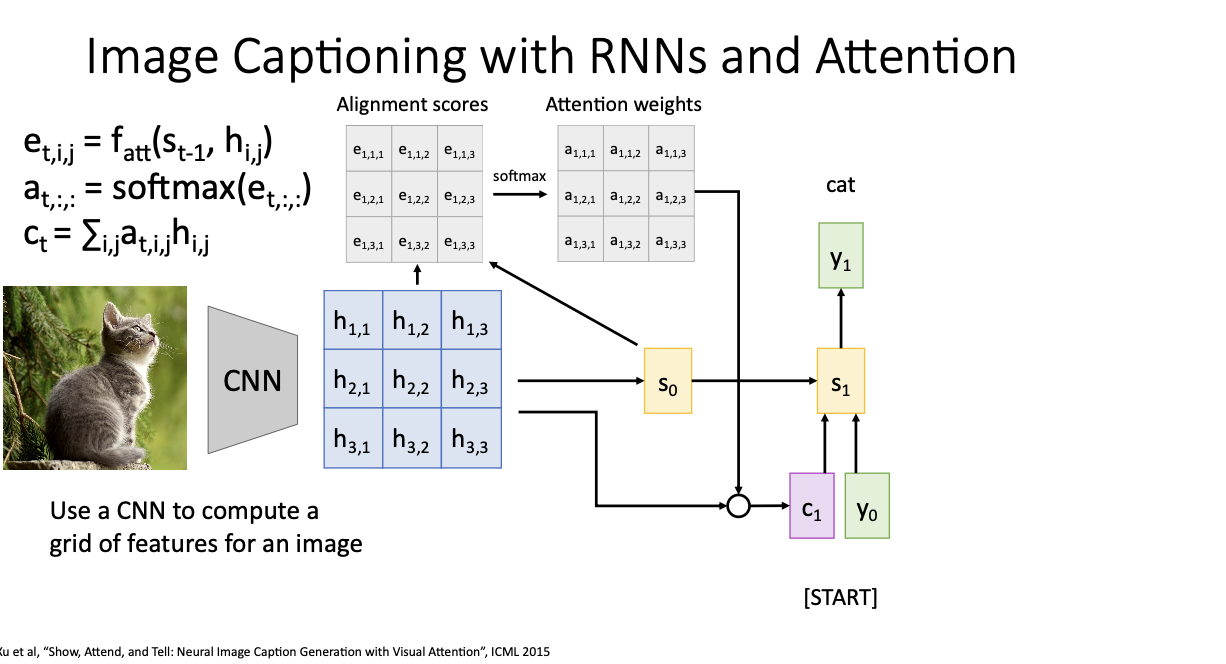
c1을 구했으니 y0(여기서는 <START>라는 토큰)와 s0을 가지고 s1을 만든 다음, s1을 가지고 y1을 출력을 하면 단어가 나오는 것이다. 이 경우에서는 고양이라고 하는 시각적 정보가 담겨 cat이라고 나오는 것을 볼 수 있다.
위 과정을 반복하여 아래와 같은 image captioning을 진행하게 된다.
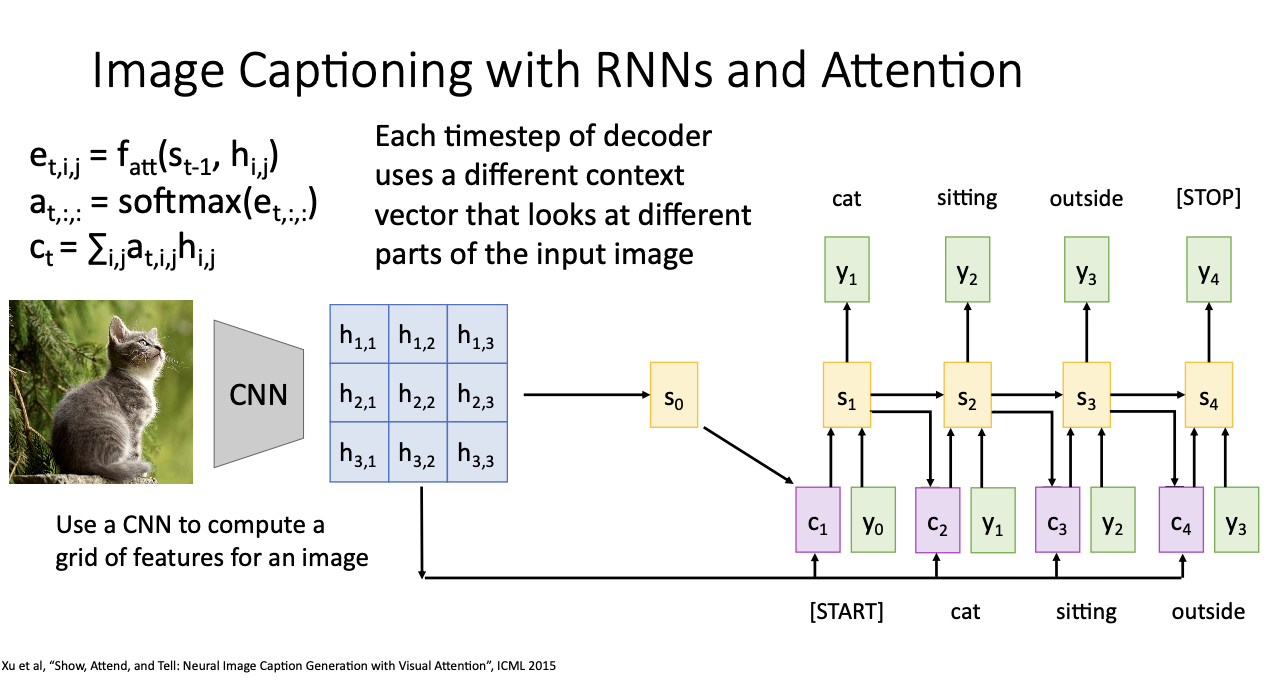
수만번 반복하는 말 같지만.. 결국 decoder의 각 time step에서 서로 다른 context vector를 사용해서 input image의 다른 부분들을 보는 것이다.
그 예를 본다면
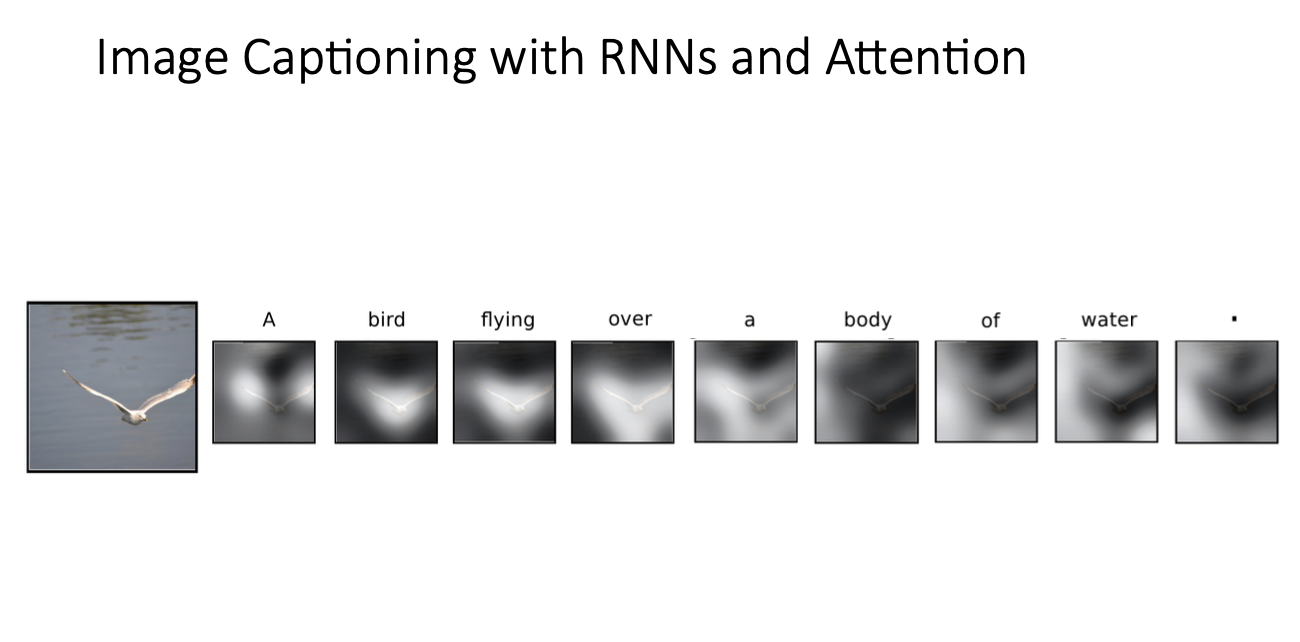
이런 입력 이미지가 있다면 "a bird flying over a body of water"이라는 문장을 만들게 된다.
하얀색으로 된 부분이 attention된 것이라고 볼 수 있는데, 새가 하나! 라는 것을 두 날개를 보고 파악, 그리고 몸통을 보고 bird를 알고..
또한 새 부분을 제외한 배경을 보고 water이라고 하는 것이다.

위 예제에서도 어떤 부분에 attention되는 지를 보여주고 있다.
왜 이러한 메커니즘을 image captioning에 사용하는 것일까? 라고 한다면 생물학적으로 생각해보자
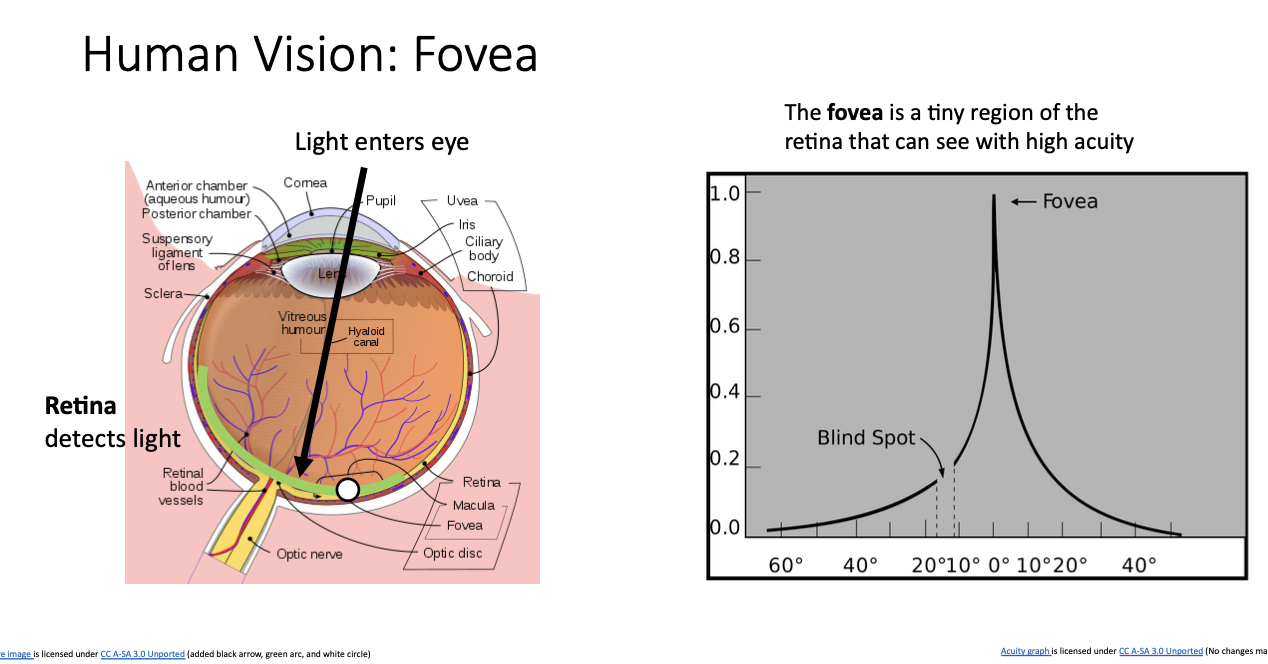
인간의 눈 다이어그램을 상상해보면 인간의 눈이 구이고, 한쪽에는 빛이 들어올 수 있는 렌즈가 있다는 것을 알 수 있다. 눈의 뒤에 있는 망막이라고 부르는 영역에서는 렌즈를 통해 들어온 빛이 맺히게 된다. 이 친구는 photosensitive cells를 가지고 있어 빛을 감지하여, 광각 세포로 얻은 신호가 두뇌로 보내져 우리가 보고 있는 것들을 보게해준다.
그치만 모든 부분의 신호가 동등하게 보내지는 것이 아니라, 망막 중간에 있는 Fovea라는 친구가 민감하게 반응하는데,
위 그래프에서 y축은 시각적 활성, x축은 망막의 위치를 나타낸다. 멀리 있으면 시각 활성이 낮고 fovea에 가까워질수록 시각 활성이 증가하는 것을 볼 수 있다. 따라서 fovea에서 가장 활성화 되었다가, 다시 멀어져 망막 끝에 다가가면 내려가서 시각 활성이 작아지게 된다.
그런데 사람은!

가만히 있어도 스무스하게 있지 않고, 계속 깜빡이면서 움직이게 되는데 그러한 현상을 Saccades motion이라고 부른다.
따라서 어떤 물체를 정상적으로 보고있는 것처럼 느껴지더라도, 계속 움직이면서 여러 시각적 장면들을 가져오게 된다.
그래서 이러한 현상들을 Attention하는 과정에서 본다면

우리가 어떤 부분들을 빠르게 다른 장면들을 보고있는 것은 Attention을 활용하여 image captioning model을 사용할 때 각 time step마다 빠르게 다양한 위치를 훑어보는 것과 비슷하다고 볼 수 있다.

- "Show, attend, and tell"
- 이 아이디어를 첫번째로 소개한 논문으로, 이미지를 보고 어떤 영역에 attend 할 지, 그 시점에 무엇을 보았는지 단어를 생성했다.
- 논문 제목이 워낙 기억하기 쉬워서.. 다른 사람들도 이런 식으로 제목을 짓기 시작했답니당
- "Ask, attend, answer" or "Show, ask, attend, answer"
- 위와 같은 논문도 제목을 보면 어떤 연구를 했는지 알 수 있다.
- 이미지를 보고, 그에 대한 질문이 주어진다면 이미지의 다양한 부분 또는 질문에 집중해서 대답하는 형식이겠다.
- "Listen, attend, and spell"
- 음성 처리를 통해 어떤 단어를 발음한 것인지 만들어내어 입력 오디오 파일의 어느 부분에 집중할 것인지를 나타내겠다.
기본적으로 한 유형의 데이터를 다른 유형의 데이터로 변환하고, 한 번에 한 단계씩 시간이 지남에 따라 수행하려는 경우 위와 같은 attention 매커니즘을 사용하는 것을 알 수 있다.
이를 일반화 시켜서 우리는 attention layer가 있다! 라고 볼 수 있는데

Input
- Query vector : q
- decoder에서 현재 내가 가지고있는 hidden state를 말한다. 즉 St !!
- Input vector : X
- 앞에서 본 hij의 grid에 해당
- Similarity function : fatt
- 위의 query vectro q (s1)와 input vector X (hij) 중 가장 유사한 h가 무엇인지! 계산
Output
- Output vector : y
- attention weights인 a와 input vector X의 곱의 합의 형태로 구하게 된다. 즉 s2!
Attention layers는 위와 같이 총 3개의 Input과 1개의 output을 가지고 있다.
Similarity function
- dot product
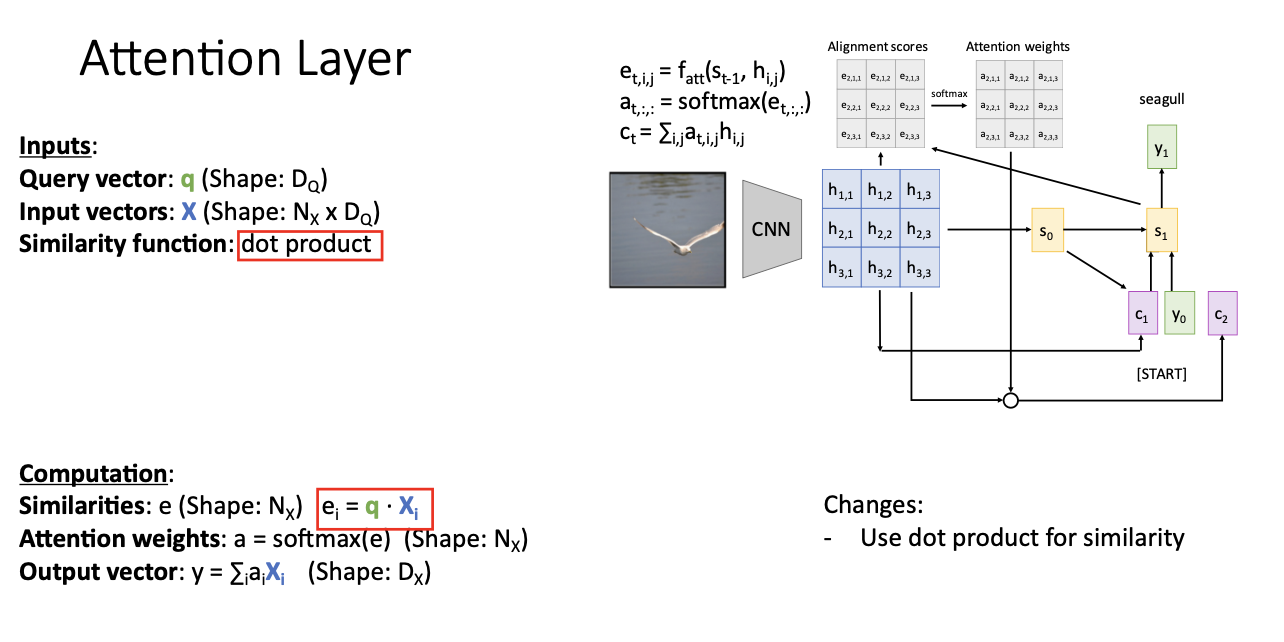
가장 간단하게 사용하는 방법은 dop product를 사용하는 방법이다.
사진을 보며 설명하면 s1과 h1,1을 곱하고, s1과 h1,2를 ,, 쭈욱 곱해 나가는 과정을 말한다.
- scaled dot product

query vector의 차원인 Dq 제곱의 형태를 나누는 방식으로 scale이 진행되는데, Similarities가 굉장히 큰 값이 있으면 softmax를 적용하고 나면 saturate가 되어버리는 현상이 나타난다. 그러면 vanishing gradient 현상이 발생하여 scaling을 해주는 것이다.
또 다른 문제로 아주 고차원의 벡터를 다루는 형태라면 dot product의 크기도 매우 커지게 된다. 따라서 이를 상쇄하기 위해 제곱근으로 나누어주어, 차원의 크기에 따라 조정되는 것이다.
하지만 여기서 quert vector가

위와 같이 Nq X Dq 의 형태라면 dot product 형태가 아닌 matrix의 곱의 형태로 나타날 것이다.
지금까지 본 것들은 decoder의 각 time step마다 하나의 query vector를 사용하였다. 즉, 하나의 쿼리를 가지고 입력 벡터 전체에 대한 확률 분포를 생성하는데 사용하였는데, 이제는 여러 query vector의 집합을 가지고 일반화를 시켜보는 것이다.
따라서 output vector 역시, 각 qurey vector에 대해 각 output vector가 만들어질 것이다.
위와 같은 연산들을 행렬 형태로 다룰 수가 있는데, 추정한 attention wieghts a와 input vector X 사이의 하나의 matrix multiplication으로 이 모든 선형 결합을 동시에 계산할 수 있다.
Input vector

input vector X를 key와 value로 나누어서 생각해 보려고 한다.
Key vector K는 input vector였던 X에 어떤 가중치 행렬을 곱하여 구하고 Value vector도 동일한 방법으로 구하게 된다.
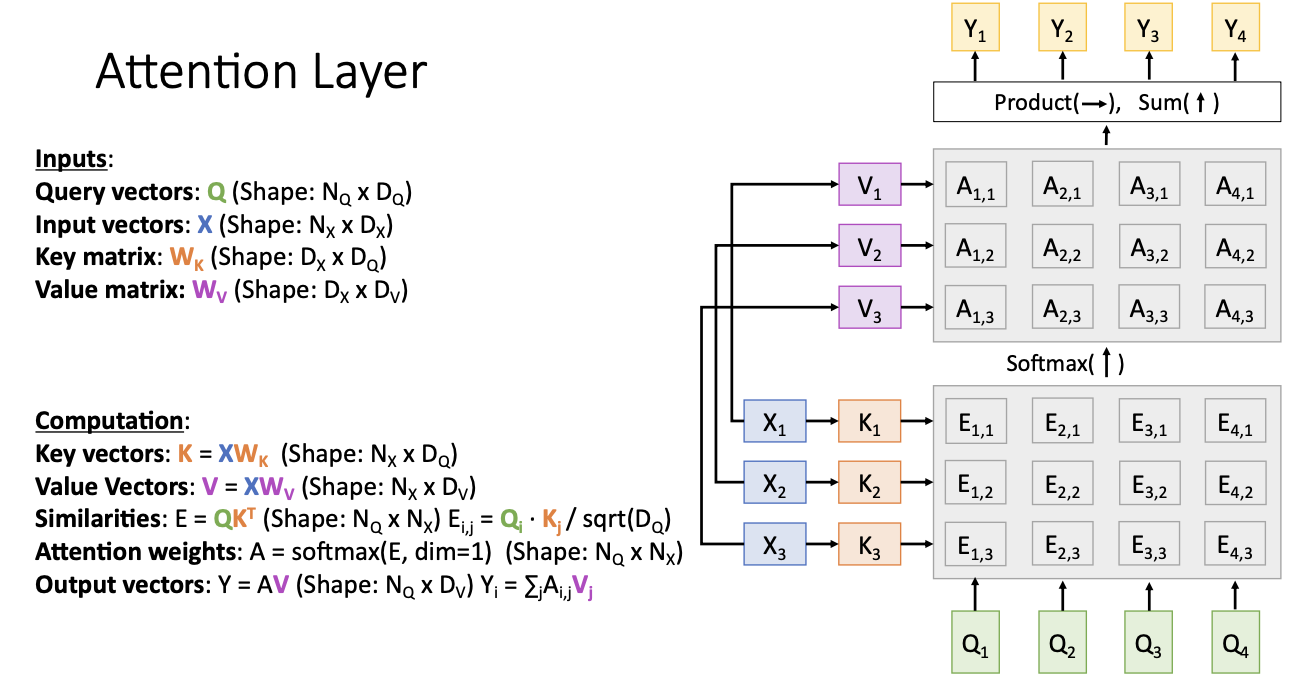
- Q가 들어오면 우리는 multiple query를 사용하고 있으므로 Q1, Q2, Q3, Q4가 있는 것을 볼 수 있고, input vector X1, X2, X3 가 있으며 그것에 대해 key와 value로 나누어 key K1, K2, K3를 위와 같이 나타낼 수 있다.
- 그럼 여기서 key와 query에 대한 similarity를 계산하여 위와 같이 Eij를 구할 수 있다.
- 구해진 Eij를 softmax를 씌워 attention weights인 Aij를 구하게 된다.
- 여기서 softmax 연산이 행렬 E의 수직 차원으로 수행되어 각 coulmn은 입력 x1, x2, x3에 대한 확률 분포가 된다.
- 다음 value를 이용해서 attention weigts의 합을 통해 output vector y를 구하게 된다.
- 이전에는 바로 input vector X와 a의 시그마를 통해 구했음!
Self-Attention Layers
self-attention은 input vector마다 각 하나의 query를 가지고 있다! 는 개념이다. 즉 입력에 관한 것 끼리의 관계도 보겠다! 라는 것.

따라서 query는 input vector X를 통하여 즉 Wq를 통하여 구하게 된다.
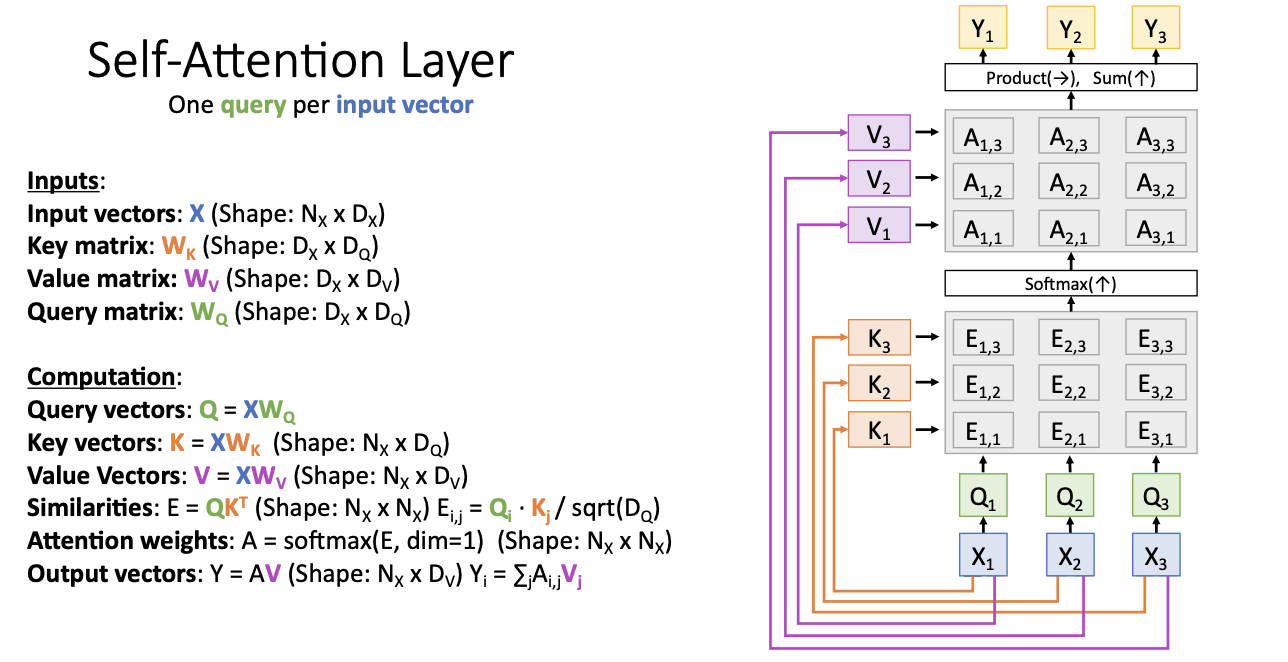
- 그런 다음은 위의 attention 과정과 같이 input X에 대해서 key vector를 구한 뒤,
- key와 query에 대한 simliarity를 구하는데
- 이때 전에는 decoding 하는 곳에서의 query와 input을 가지고 유사도를 구했다면
- 지금은 input 사이의 관계에 대한 유사도를 계산하게 된다.
- softmax를 통하여 attention weigths를 구함.
- 다음 value를 통해 output을 계산한다.
여기서 셀프 어텐션의 놀라운 점을 알 수 있는데! input vector의 순서를 바꾸어보면 된다.
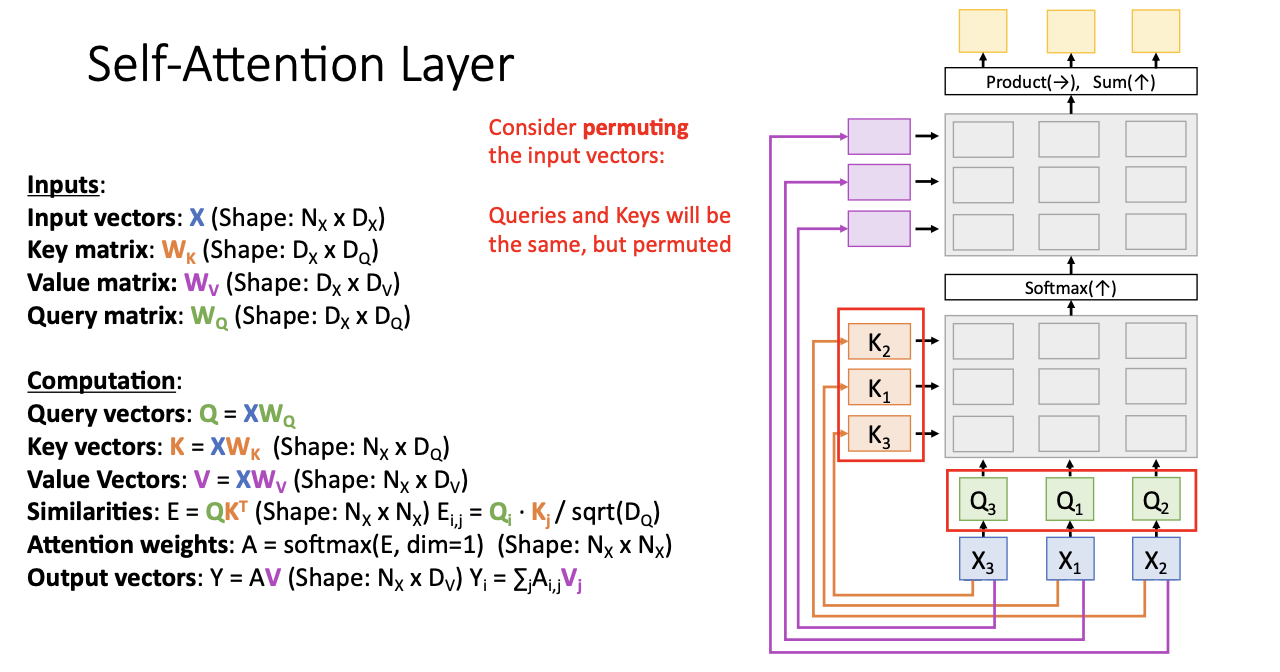
X1, X2, X3이 아닌 3, 1, 2 순서여도 key와 query는 서로 영향을 주지 않기 때문에 동일한 key vector와 동일한 query vector를 구하는 것을 볼 수 있다.
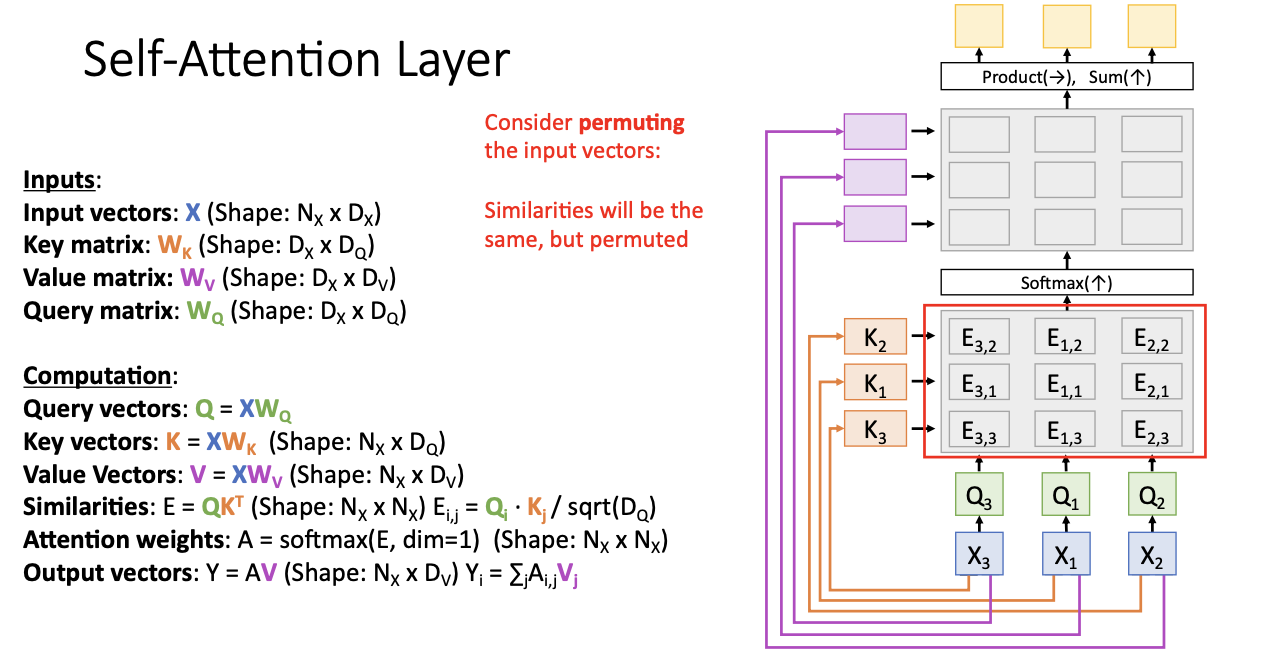

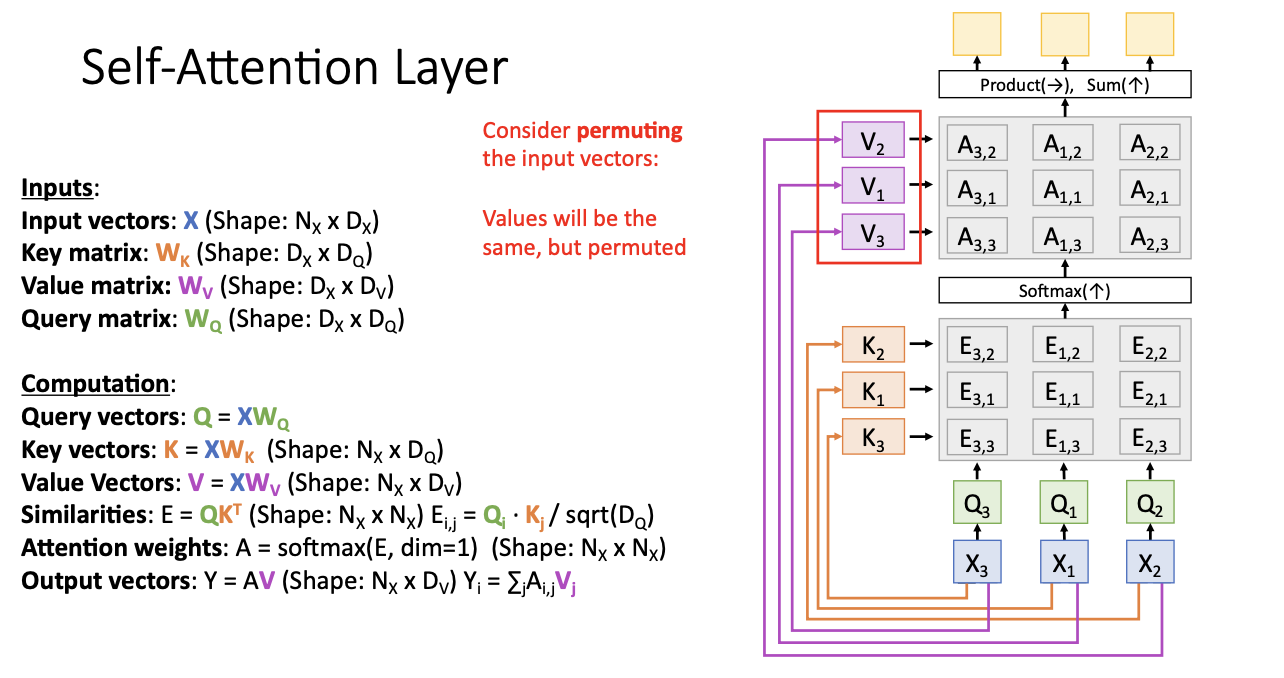

또한 뒤바뀐 vector들 사이에서 유사도 스코어, attention wieghts, value vector, output vector 모두 를 계산할 때, 모든 값은 동일! 하지만 행과 열이 바뀌었으므로 이 행렬과 벡터 자체도 뒤바뀌게 된다.
이러한 현상이 의미하는 것은
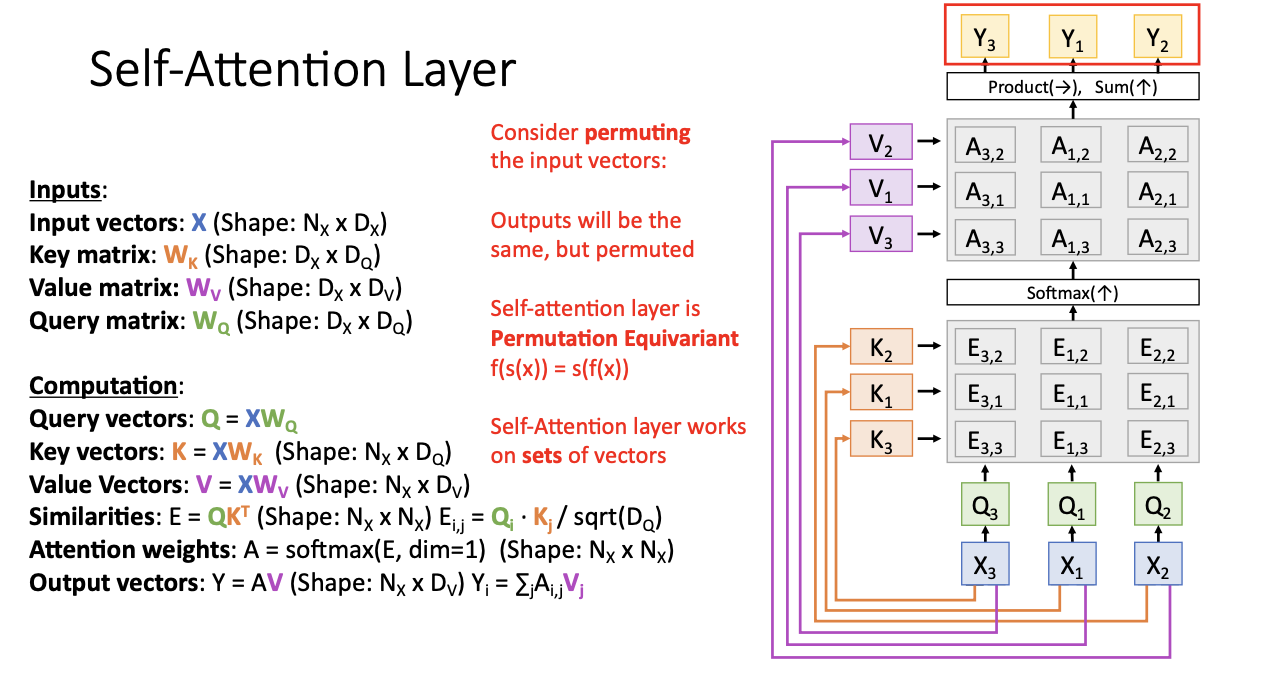
self-attention layer와 연산 등은 동등치환! 동일하나 순서를 바꾸는 것! 이다.
즉 입력의 순서를 상관하지 않으므로 순서를 고려하지 않는다는 점에서 새로운 종류의 신경망 계층이기도 하며, 벡터의 집합만을 가지고 연산하겠다는 의미를 가지고 있다.
즉! 그냥 여러 벡터들 x를 가지고 각 q, k를 서로서로 비교하여 새로운 벡터 집합 y를 구하는 과정이라고 할 수 있다.
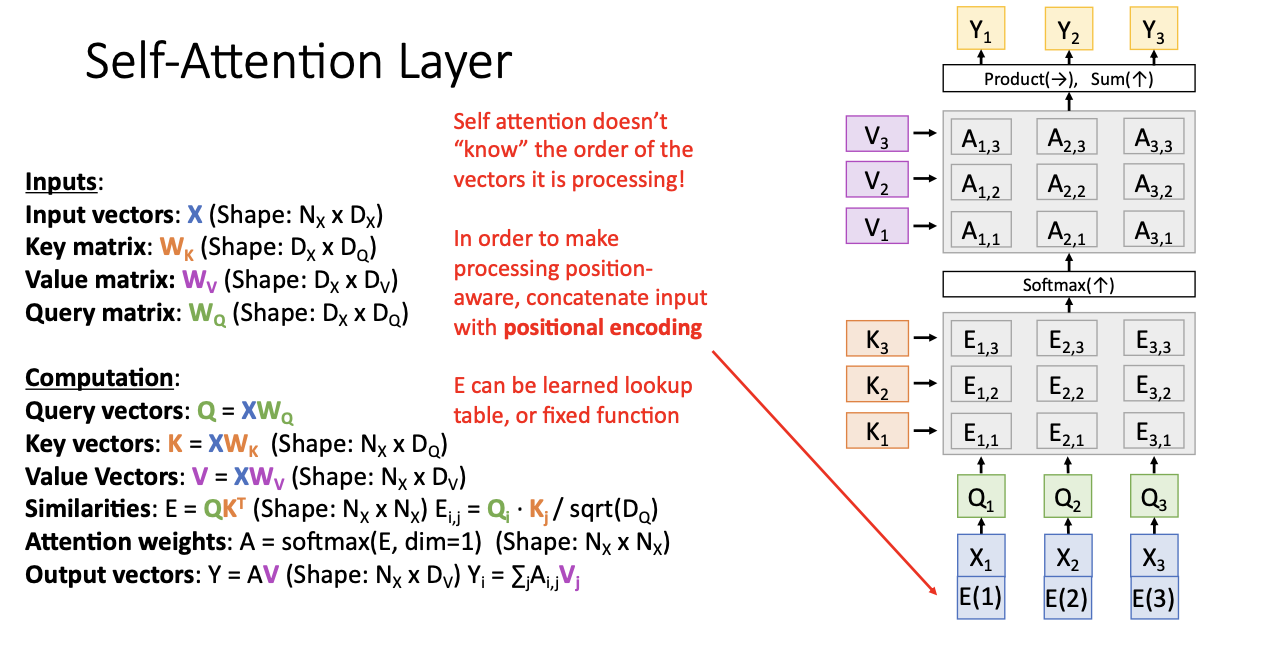
그래서 우리는 이 layer에서 input vector를 처리할 때 그 벡터들의 순서가 어떻게 되는 지 알 길이 없는 것이다.
근데 task에 따라서 벡터가 어느 위치에 있는지 아는게 중요한 경우도 분명 있을 것이다. 하지만 셀프 어텐션은 동등치환이므로,
어떤 벡터가 첫번째이고 어느 것이 맨 마지막인지 알 수 없다.
따라서 위와 같이 벡터의 위치를 encoding하는, positional encoding을 진행하여 위치 정보를 input과 함께 넣어준다.
신경망에다가 학습 가능한 가중치 행렬을 추가하여 벡터 하나로 첫번째 위치를 학습하고, 다른 한 벡터로 두번째 위치를 학습, 다른 세번째 벡터로 세번째 위치를 학습하여 forward 연산을 수행할 때, 첫번째 벡터 아래에 학습한 벡터를 붙이고! 두번째 forward 할 때, 첫번째 벡터 아래에 학습된 위치 벡터를 붙이는 방식으로 진행된다.
이로써 sequence의 각 부분들이 시작 부분인지, 끝 부분인지를 구분할 수 있게되는 것이다.
또한 self-attention의 변형으로!
Masked Self-Attention
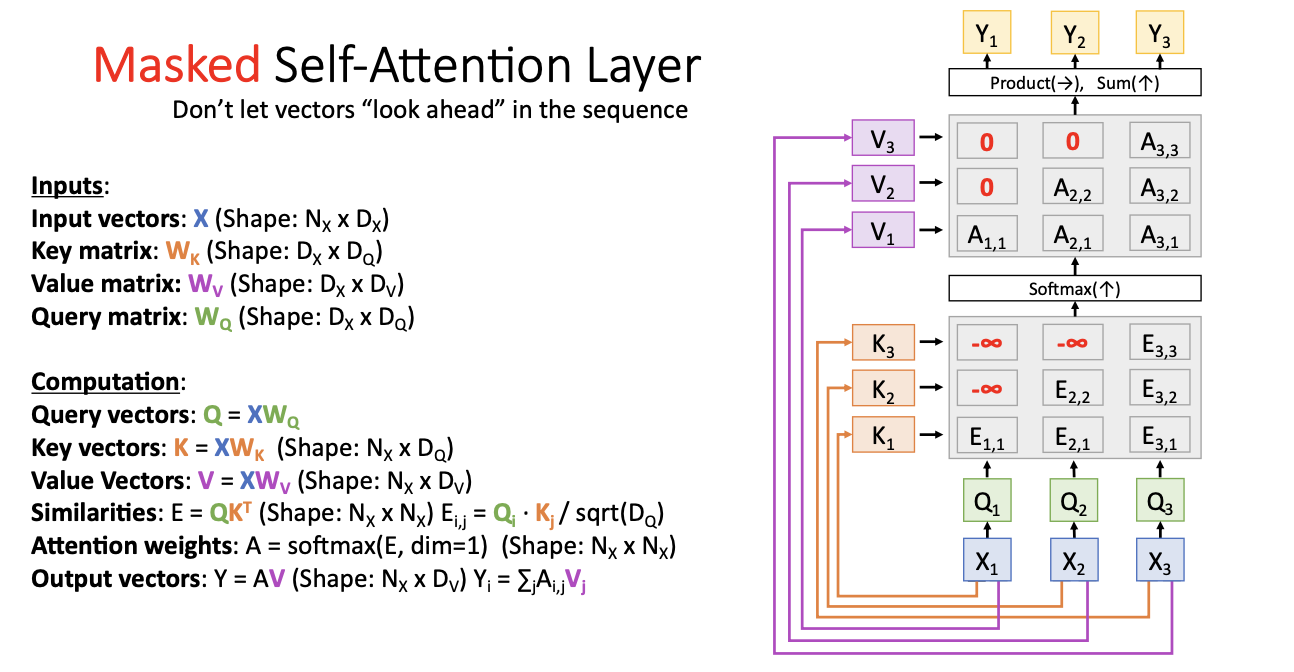
순서적으로 진행할 때 X1에 대해서 처리할 때에는 X2, X3에 대해서는 보지 않고 X1에 대한 key를 가지고 유사도를 계산한다.
그 다음 X2에 대해서 처리할 때에는, 이전 layer도 함께! 즉 X1과 X2에 대해서만 생각하고 X3만 보지 않겠다는 것이다.
즉 모델이 이전의 정보만 사용하기를 원할 때 사용되는데, 언어 모델링의 경우에 자주 사용될 것이다.
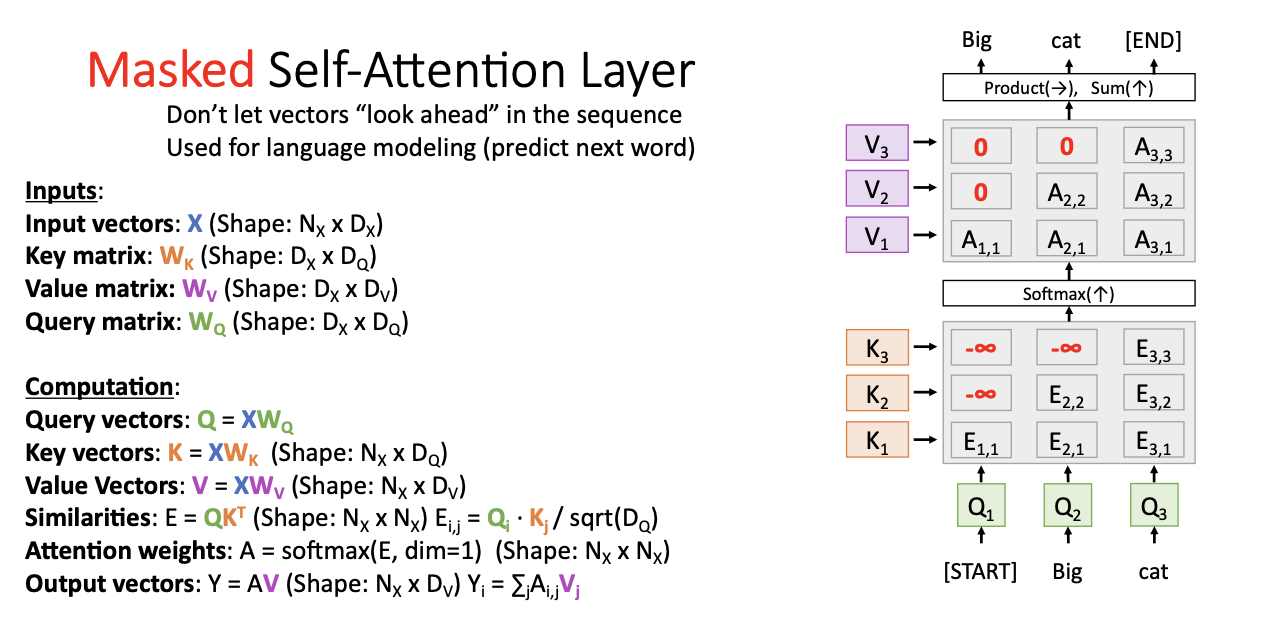
위와 같이 laguage modeling에 적용해보면, "look ahead"! 앞을 내다보는 현상을 방지하기 위해 mask를 씌운다고 이해하면 된다.
- 음의 무한대로 mask를 씌우는 이유는?
- 음의 무한대로 넣어 softmax함수를 거치게 되면 attention weights의 값들이 0이 되어 영향을 미치지 않기 때문에!
다음 또다른 변형인
Multihead Self-Attention
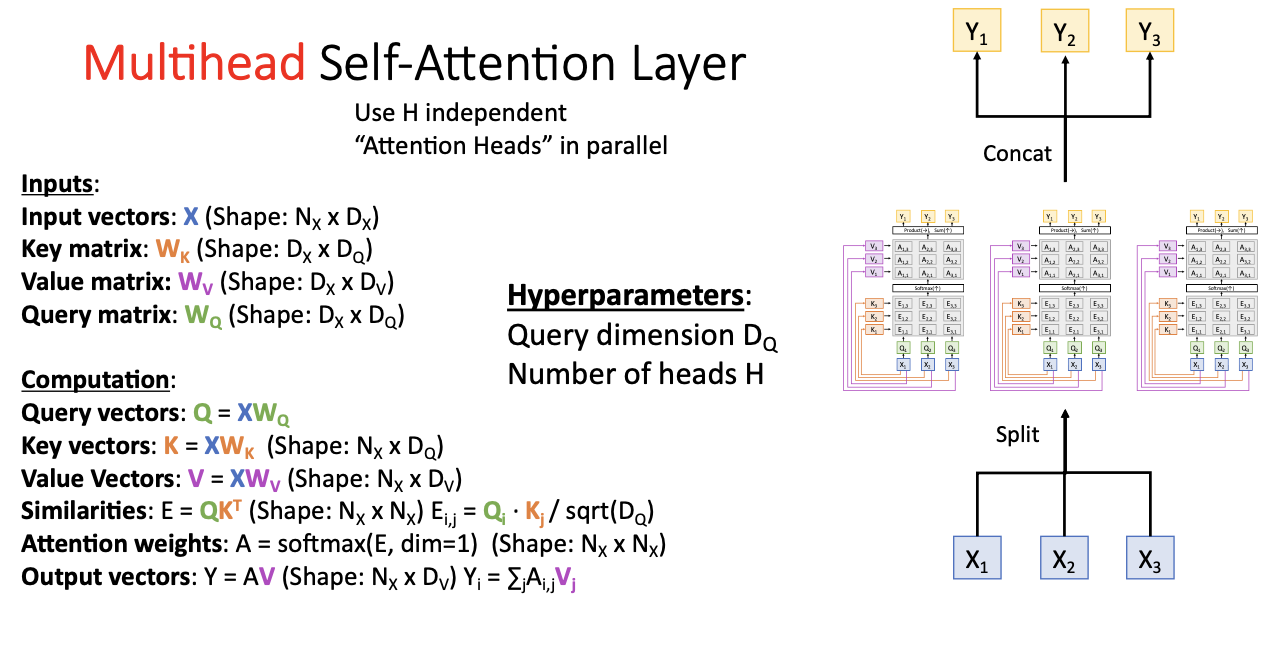
이 방법은 head의 개수 h를 지정하고, self-attention 레이어를 병렬로 독립적으로 동작시켜 입력 벡터를 분할해서 주는 것이다.
이때 input vector X가 d차원이라면 각 input vector들을 동일한 h개의 덩어리로 분할시켜 준다.
각각의 input vector 덩어리들을 병렬화된 self-attention에다가 넣어주고, 각 하부의 셀프 어텐션 레이어는 각 입력에 대해 각 출력을 만들어내어 이러한 multihead self-attention layer로부터 최종 출력을 얻기 위해 각 출력들을 연결시킨다.
이는 실제로 자주 사용되고 있으며, 이때 우리는 두가지의 hyper parameter를 가지게 된다.
- query vector의 차원
- 최종 output의 차원
이 모델에서 내부적으로 지정해주어야 하는 hyperparmeter는
- ket vector의 차원
- head의 개수
그렇다면 이제 실제 CNN을 가지고 Self-Attention을 하는 예를 보자.

우리의 featuers 가 channels, width, heigth 로 이루어져있다고 할 때,
- Queries, Keys, Values
- 1x1 conv를 통해 동일한 차원(C')을 만든다.
- 1x1 conv가 무슨 역할을 하는데?
- 학습 과정으로 얻은 고유의 가중치와 편향값을 가지고 있어 병렬로 분할시켜준다. (?)
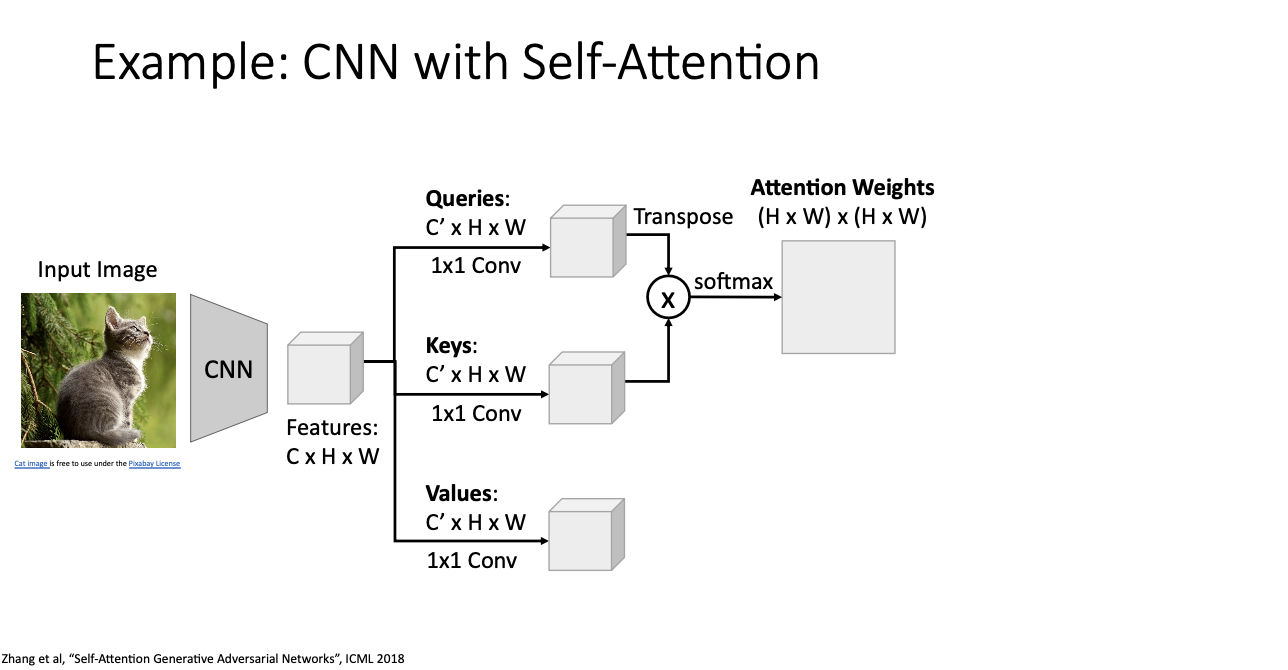
- Attention weights
- query와 keys를 가지고 유사도를 구한 뒤 softmax를 통해 Attention Weight를 구한다.
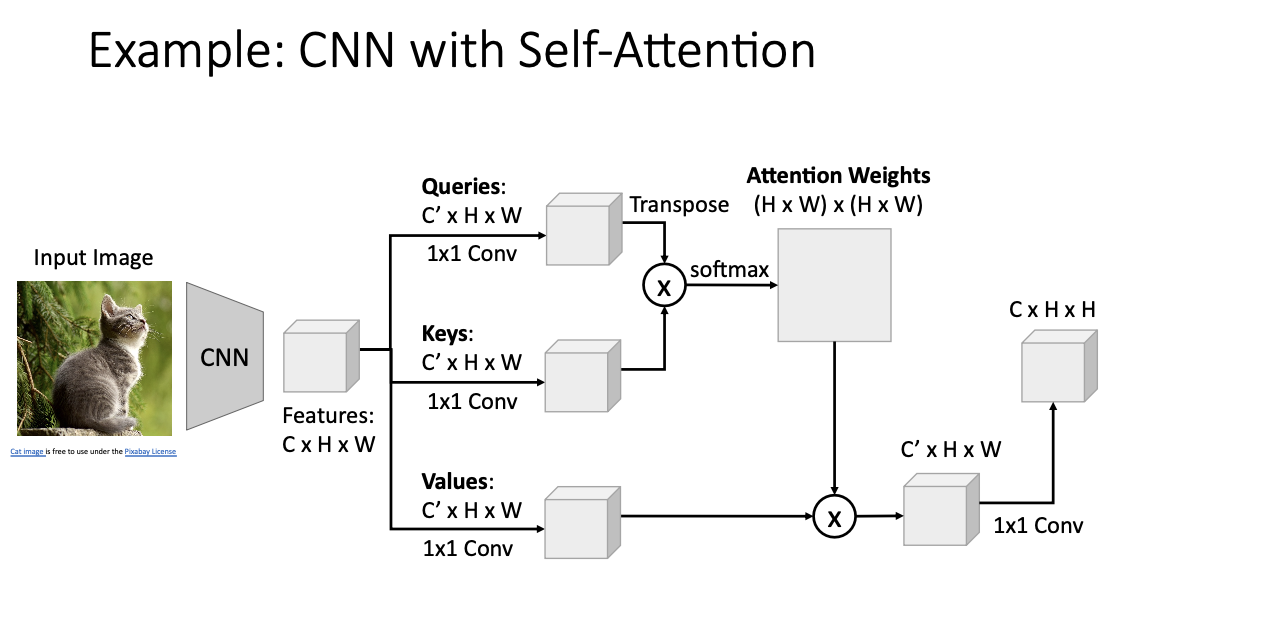
- Output
- attention weights와 values를 통한 값에다가 다시 1x1 conv를 통해 CxHxW로 구해낸다. (그림 오타!)
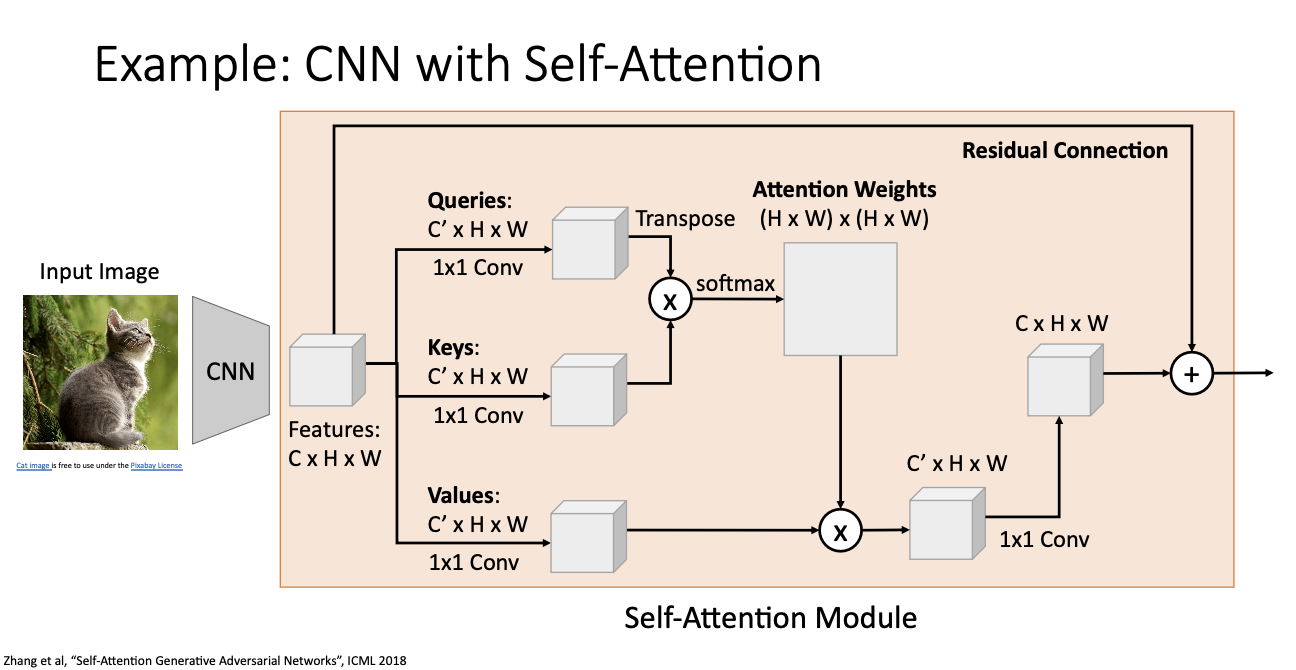
- Residual Connection
- 일반적으로 네트워크의 입력과 출력을 더하는 방식을 말하는데, x + F(x)라 할 수 있다. 이러한 구조는 gradient가 뒤로 흐를 때, 두 부분이 더해지므로 기존의 입력이나 특성이 더해져 gradient의 손실을 완화하고 학습을 돕게된다.
앞선 포스팅에서 언급했던것과 합쳐 squences를 처리하는 방법들을 정리해보자.

- Recurrent Neural Network
- input vector들의 sequence x가 주어지면, output vector y의 sequence를 만들어냄.
- 장점 : 아주 긴 sequence에 대해서도 정보를 잘 전달함.
- 단점 : hidden state는 순서에 의존적이라 병렬화 시키기가 어려움. -> GPU 비효율적!, 큰 모델 만드는데 문제
- 1 x 1 Convolution
- 일차원 convolution을 통해 input sequence를 slide시켜 인접한 것들을 통해 출력 sequence의 각 지점들을 구할 수 있다.
- 장점 : 순차 의존성이 없어 독립적으로 계산하여 병렬화 하기 좋음
- 단점 : 매우 긴 시퀀스를 처리하지 못 함! -> 모든 지점을 지나기 위해 너무 많은 layer를 쌓아야 함
- Self-Attention
- 벡터의 집합으로 처리하는 메커니즘
- 장점 : 주어진 벡터의 집합으로 각 벡터와 다른 모든 벡터를 비교하여 긴 시퀀스도 잘 처리! 몇 개의 행렬 곱 연산과 softmax로 이루어져 있어 병렬화 하기 좋아! -> GPU에서 연산하기 적합!
- 단점 : 아주 많은 메모리 공간을 사용
- 그런데 시간이 지날수록 GPU의 메모리 공간은 더 커지고 있어서 ㄱㅊ!
유명한 논문 "Attention is all you need"인데 ..

뭐 결론은!
신경망으로 sequence를 처리하고 싶으면~ Attention! 을 사용해라! 이다.
와앙 드디어 끝낸 Attention-1!
봐 뉴진스 어텐션 아니랬지?
다음은 2로 돌아오께
설 날 연휴인데.. 광양인데..!
일어나자마자 스터디 카페 왔어..
그렇지만 최대 효율이었우니까 낼도 올게(?)
다들 새해 복 주섬주섬 챙기가
새복많 💰
'EECS 498-007' 카테고리의 다른 글
| [EECS 498-007] Lecture 14. Visualizing and Understanding (6) | 2024.02.18 |
|---|---|
| [EECS 498-007] Lecture 13-2. Attention (1) | 2024.02.12 |
| [EECS 498-007] Lecture 12. Recurrent Neural Networks (3) | 2024.02.03 |
| [EECS 498-007] Lecture 10. Training Neural Networks I (2) | 2024.01.29 |
| [EECS 498-007] Lecture 09. Hardware and Software (2) | 2024.01.25 |