오늘은 두번째 시간 ... 3강! 리니어 클래시피어 이당
많이 많이 엄청 엄청 자주 자주 들어봤지만 자신만만하게 강의를 켰지만
항상.. 그 때마다 배워가는 건 참 많당.. 겸손해야함 흐히
아침부터 작성하려니 졸림 max얌
그치만 화이팅 해부께
Linear classifier는 선형으로 어떤 무언가를 분류해주는 알고리즘이다.
신경망 모델의 개별 요소가 linear classifier와 유사하다고 한다.
머신러닝을 공부하다 보면 자주 들어봤을 parametric approach 개념이 등장한다.
| Parametirc Approach | None Parametric Approach |
| parameter 값만 저장하는 방식 | 모든 데이터를 저장 |
| ex) linear classifier | ex) knn |
그리고 앞서 2강에서 소개했던 CIFAR10 data가 등장하는데 이 강의에서는 이 데이터를 활용하여

input image가 들어오면 비행기, 자동차. 고양이 등 10개의 클래스에서 알맞은 클래스로 분류해보자! 를 하고싶은 것이다.
1. input image : 우리의 원래 이미지의 크기인 32x32x3을 flatten 하여 3072 x 1의 형태로 바꾼다.
* 여기서 flatten이란! 이미지 픽셀을 긴 열벡터 형태로 늘리는 과정을 말한다. 모든 공간 구조가 파괴되는 특징이 있다.
2. f(x, W) = Wx + b : 입력 이미지에 대해 flatten을 마친 후, 함수에 넣어준다. 우리는 10개 클래스 각각에 해당하는 점수를
출력으로 얻어야 하므로 10개의 클래스에 대한 점수값을 출력해야 한다.
즉, input의 shape이 (3072, 1) 인데 output의 shape은 (10, 1)이어야 함!
그렇다면 W는 (10, 3072)의 shape을 가져야 하겠구나!

3. 가중치(W) : (10, 3072) 형태에서 10은 우리가 나누려는 클래스의 개수가 되며, 3072는 이미지 픽셀의 수가 된다.
즉, 10 x 3072의 2차원 가중치 행렬이 된다.
4. bias : 모델이 편향을 고려하여 더 나은 학습을 할 수 있도록 돕기위한 친구이다. 항상 모델이 원점을 지나는 한계를 극복시켜준다.
Linear Classifier를 바라보는 3가지 관점
1) Algebraic Viewpoint
대수적 관점에서 바라보자! -> 행렬과 벡터의 곱으로 이해해보자!

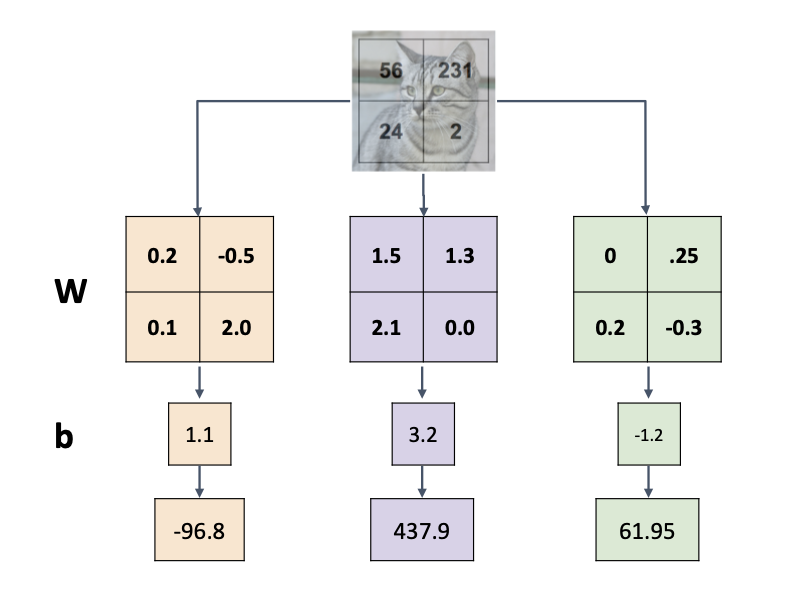
1. input image(2x2)를 flatten pixel into column을 진행하여 열벡터의 형태로 나타내기
2. W(3x4) 3: 클래수의 개수, 4: 이미지 픽셀의 가중치 행렬을 생성하기
3. input image와 가중치 행렬과 벡터 내적 연산을 수행한 뒤, 마지막에 bias를 더하여 각 클래스의 점수를 계산하기
여기서 * bias trick을 적용할 수 있다.
*bias trick이란, bias를 따로 떨어진 상수항으로 취급하지 않고 가중치 행렬의 포함시켜 계산하는 것을 말한다.
이 때 열벡터의 크기는 뒤에 1을 추가시켜 (5, 1)이 될 것이다.

이 방법은 상수항을 없앰으로써 단순한 구조를 만들어 이해를 돕는다는 장점이 있다.
하지만 CV에선 잘 사용하지 안흔ㄴ다. linear classifier에서 convoulution으로 이동할 때 잘 적용되지 않으며
컴퓨터 비전에서는 데이터가 복잡한 구조를 갖는 경우가 많아 비선형적인 구조를 띈다.
더하여 파라미터들을 초기화 혹은 정규화 할 때 가중치와 bias를 따로 분리하는 것이 유리하다는 점을 이유로 들었다.
대수적 관점에서 바라보았을 때 가장 큰 특징은 예측이 선형이라는 점이다.

입력 이미지에 상수 곱의 변화가 생겼을 때 선형적으로 반영이 된다는 것이다.
위 그림처럼 입력 이미지에 0.5를 곱해 채도를 낮춘 상황에서 각 출력되는 점수 또한 0.5배가 되었다.
2) Visual Viewpoint
다음은 시각적 관점에서 linear classifier를 바라보아보자~
가중치 행렬의 각 행의 이미지와 동일한 shape을 가지도록 하는 것이다.
가중치 행렬의 각 행이 이미지와 동일한 shape을 갖기 때문에 시각화에 강인하고, 총 10개의 템플릿이 생성됨을 알 수 있다.

아래 10개의 템플릿이 생성되었음을 볼 수 있다.
템플릿을 유심히 바라보아보자!
비행기 템플릿을 보면 가운데 무언가 있으며 전체적으로 파랗고, 사슴 템플릿은 가운데 갈색의 무언가가 있고, 녹색 배경을 가지고 있다.
이는 linear classifier의 실패 요인과도 연결되는데, 숲속에 주차된 차 이미지가 입력 이미지로 주어진다고 생각해보자.
차 형태의 car 템플릿에는 잘 매칭되겠지만 녹색 배경은 사슴 템플릿에 더 잘 매칭되기에 linear classifier 입장에서는 무엇으로
분류해야 할 지 확신이 서지 않을 것이다.
두번째로 꼽을 수 있는 실패요인은 말의 템플릿을 보면 알 수 있다.
요점은 linear classifier가 하나의 클래스 당 하나의 템플릿만 학습할 수 있다는 것이다.
말은 왼쪽을 보고 있을수도, 오른쪽을 보고 있을수도 있다. 하지만 서로 다른 방향을 보고있는 말에 대해 각기 다른 템플릿으로 학습할 수 없으므로 머리가 2개가 달린 템플릿이 생성된 것이다.
머리가 2개인 말 ... 은 문제가 있을테니깐 ..
3) Geometric Viewpoint
마지막으로 기하학점 관점에서 linear classifier를 바라볼 것이다.
나는 이 섹션이 이해하는데 참 .. 어려웠다. 옛날부터 기하학적 사고엔 영 소질이 없는듯 하다..........

왼쪽 그래프가 나타내는 의미는 특정 픽셀 15, 8의 R채널에서의 분류기 점수를 나타낸 그래프이다.
Car Score만 해석해보자면 R채널의 값이 많아질수록 Car Score의 값은 올라가는 것이다. -> 왜냐! 빨간색 차였거든!


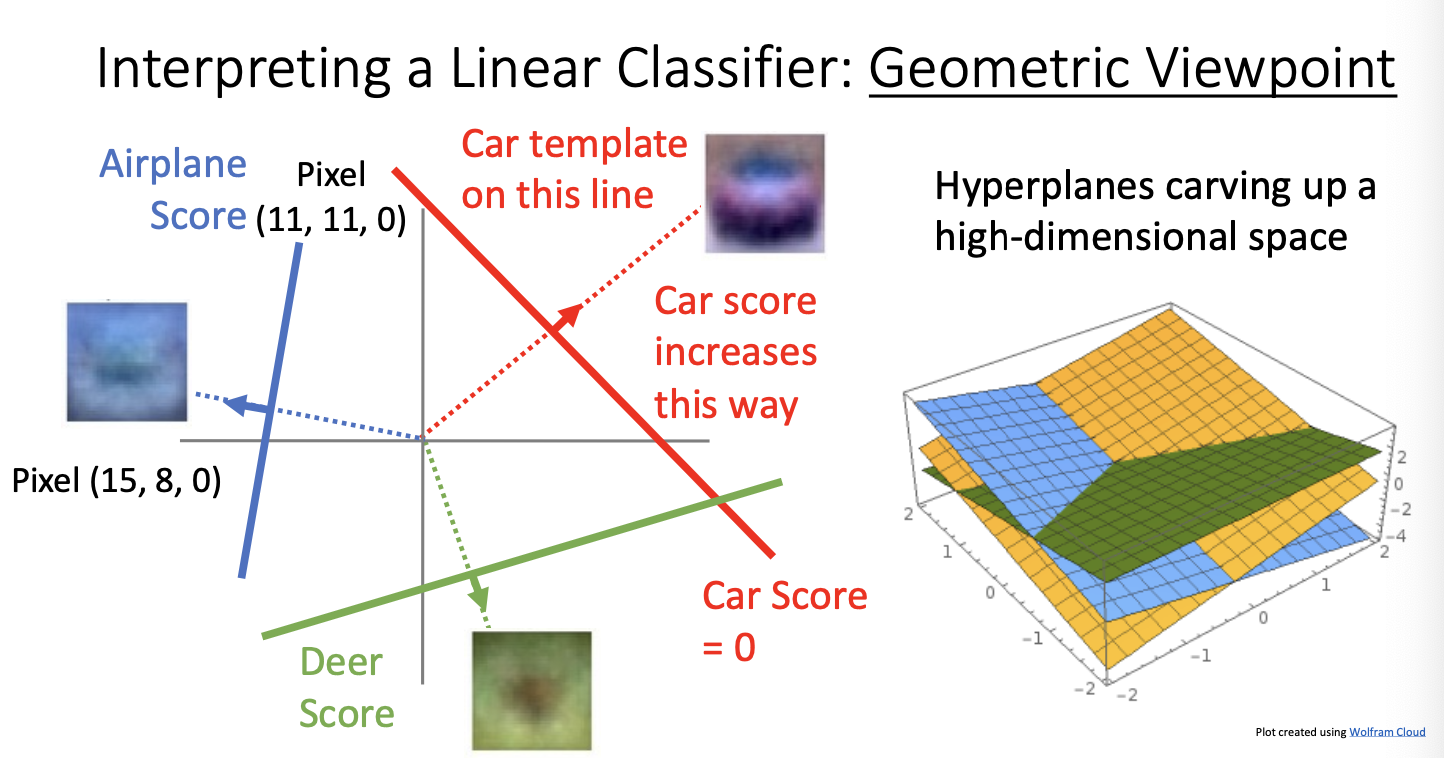
다음은 두가지 픽셀을 x축과 y축에 대응시켰을 때의 score를 나타낸 것이다.
car score가 0.5가 되는 선을 그은 뒤 그 선에 수직인 방향으로 car score가 선형적으로 증가하게 될 것이다.
따라서 car 템플릿은 그 수직선 위에 있게 될 것이다.
이를 2차원이 아닌 고차원으로 확장한다면 직선을 넘어 초평면으로 표현될 것이다. 그게 3번째 사진을 의미!
다음은
Hard Cases for a Linear Calssifier
선형 분류기의 한계를 말 할 것이다. 선형 분류가 불가능한 경우에는 적용할 수 없다.

파란색과 빨간색을 구분 지을 수 있는 직선이 존재하지 않는다.
지금까지 세가지 관점에서 linear classifier를 바라보았다.
이 세가지 관점에서 공통적으로 '가중치'를 곱하는 원리가 적용되었다. 그렇다면 이 가중치가 굉장히 중요해보인다..
유의미한 가중치를 찾기 위해서는 loss function을 사용하여 loss가 최소화되는 가중치를 찾으면 된다.
Loss Function은 분류기가 데이터에 얼마나 잘 작동하는지 알려주는 지표이다.
수식에 대한 설명은 건너 뛰겠슴니다 갈 길이 멀기에
1) Multicalss SVM loss
첫번째로 다룰 SVM loss는 classfication에서 보편적으로 쓰이는 loss function이다.
한 마디로 정리하면 '정답 클래스가 다른 클래스보다 최소 이정도는 높아야 한다!' 라는 아이디어 이다.

여기서
- Sj : 오답 클래스의 score
- Syi : 정답 클래스의 score
- 1 : Marjin 으로 정답과 오답의 차이가 1보다 커지는 스코어를 얻어야 loss 가 0이 되며 그 이하라면 loss가 존재하게 된다.
Cat의 경우를 예를 들어 SVM loss를 구해보자면

정답 클래스를 제외한 5.1 과 -1.7을 식에 넣게 된다.
두 클래스의 loss를 구해준 뒤 합한다면 고양이 이미지에 대한 전체 loss를 얻을 수 있다.
다른 클래스들도 같은 방식으로 계산해준 뒤 평균을 내어 loss를 구하면 전체 Multiclass SVM loss가 된다.
강의에서 SVM의 특징을 알 수 있도록 몇가지 질문을 던지는데,
Q : Score값이 살짝 변화하면 loss에 어떤 영향을 줄까?
A : 한번 바르게 예측하면 class score가 바뀌더라도 loss에 큰 영향을 주지 않을 것이다. -> 정답과 오답의 차이가 월등히 커서!
Q : SVM Loss의 min과 max는?
A : min은 0, 이론상 max는 무한대가 된다.
Q : score를 랜덤하게 초기화 한다면 어떻게 될까?
A : (c-1) * margin의 값을 얻음 => 근데 이게 무슨말이지..
Q : 만약 정답 클래스도 loss 계산에 포함된다면?
A : 모든 loss가 marjin만큼 증가하게 될 것이다. 즉 결과에는 영향을 주지 않으나, 일반적으로 loss가 0이어야 마음이 편하니(?)
굳이 포함하지 않는다고 합니다.
Q : loss 에 sum대신 mean을 사용한다면?
A : 전체적인 경향성은 해치지 않으므로 스케일만 변할 뿐 결과는 달라지지 않는다.
Q : 제곱 형태의 loss를 사용한다면?
A : 더이상 muilticlass SVM loss 라고 할 수 없으며 이는 squeared hinge loss라 한다. -> 비선형적으로 바뀌게 됨!
2) Cross-Entropy Loss
다음은 확률적 관점에서 바라보는 Cross-Entropy Loss이다. 모델이 예측한 점수가 나올 확률과 실제 확률의 차이를
측정하는 것이 그 아이디어 이다.
먼저 도출된 score에 exponential을 취한 뒤 정규화를 통해 0과 1 사이의 값으로 만들어준다.
0과 1 사이의 값으로 정규화되므로 그 합은 1이 되며 확률로써 사용할 수 있게 되는 것이다.
모델이 예측할 확률과 실제 확률을 비교한 결과를 도출하는 것이 cross entropy인 것이다.
여기서 그 둘을 비교할 때, KL- divergence를 사용한다. 대충 두 확률 분포를 비교한다는 것인데, 그 비교의 기준이 거리가 아닌 수치.. 적
스칼라 값이라고 생각하면 되겠다
** 스터디를 하면서 entropy, coross entropy, kl-divergence의 개념을 확실히 하는 것이 좋다는 조언이 있었다..
포스팅 하면서 요기조기 검색해서 감은 잡았지만(?) 아직 익숙치 않다.. 여유로울때 새로운 글에 다시 정리해보도록 하겠다!
더하여 강의에서 coross entropy와 SVM을 비교하며 몇가지 질문들을 던진다
Q : score 값이 살짝 변하면 loss에 영향을 주는가?
SVM : loss 변화 없음.
Coross-Entropy : score값을 가공하며 사용하여 loss의 변화가 있다.
Q : loss의 min과 max는?
SVM : min은 0이 되며, max는 이론상 무한대이다.
Coross-Entropy : min은 0이 되나 max는 이론상 무한대이다. 하지만 0이되는 경우는 없다고 보면 된다.
Q : score를 랜덤하게 초기화 한다면?
SVM : loss값 또한 랜덤한 작은 값
Coross-Entropy : 현재 데이터의 경우 -log(c) == -log(10) -> 약 2.3이 된다.
*c는 class의 개수
Q : 정답 클래스의 score가 두 배가 된다면?
SVM : 동일할 것
Coross-Entropy : 감소할 것이다. -> 식을 보면 -log()의 형태이므로 score가 커지면 최종적으로 loss는 감소하게 된다.
마지막은 Regularization이다.
모델을 학습시킬 때는 train data를 사용하지만 최종 성능을 발휘하는 것은 test data의 결과이다.
그런데 학습 단계에서 training loss가 0이 된다면 과도하게 적합되어 있어 test data가 들어왔을 때 오히려 loss가 커질 수 있다.
이러한 현상을 overfiting이라고 하며 많이 들어봤을 것이다.
이를 해결하기 위해 Regularization term을 추가하는 것이다.
간단한 형태로는 L1, L2, elastic net이 있으며
복잡한 형태로는 drop out, batch normalization, cutout, mixup 등등이 있다.
*스터디를 하면서 L1, L2의 차이점과, 그래서 언제 어떤걸 쓰는게 좋은지가 단골 질문이라고 하셨다. 그것을 중점으로 써내려가 보겠습니당
1) L1 Regularization

가중치의 절댓값을 사용하여 정규화하며 모델의 손실 함수에 가중치의 절댓값의 합에 특정 상수를 곱한 값을 추가한다.
특징 : 불필요한 가중치를 0으로 만들어 특성 선택을 수행하며 모델을 간소화 하는 효과가 있다.
이상치에 민감하게 반응할 수 있다.
사용 : 이미지나 텍스트 데이터 등 많은 특성이 존재하는 경우 중요한 특성만을 고려할 때
희소한 해를 얻을 때, 일부 가중치를 완전히 0으로 만들 수 있어 희소성을 중요시 할 때
2) L2 Regularization
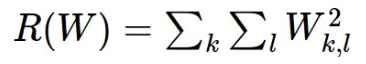
가중치의 제곱을 사용하여 정규화하며 가중치의 제곱의 합에 특정 상수를 곱한 값을 추가한다.
특징 : 중치의 크기를 줄이는 데 중점을 두며, 각 가중치의 값들을 더 조화롭게 만들어 준다.
일부 특정 특성에 지나치게 의존하는 것을 방지하고 모든 특성을 골고루 사용하는 일반화 성능을 향상시키는 데 기여한다.
이상치에 덜 민감하다.
사용 : 일반화 능력을 향상시켜야 하는 회귀문제에 자주 사용될 것.
이미지 분류나 객체 검출과 같은 모델의 복잡도가 높은 경우 일반화 성능 향상을 위해 자주 사용될 것.
아주 긴 내용을 정리해 보았다..
허술한 점 짱 많고 수정하러 많이 올 것 같지만 뿌듯?
아침에 시작했는데 짱 늦었네..
오늘 스터디 참 빡셋다 내가 발표자도 아니였는데 조금 울 것 같았음 히히
그런데 공부 방향? 바라보는 관점? 을 좀 배워간 거 같아서 유의미해 ~
냅다 2강은 포스팅 안 하고 3강 먼저 하는 사람이지만..
윤수많 ~ 아 배고파 교수님 감사합니다 치킨사주셔서
><
'EECS 498-007' 카테고리의 다른 글
| [EECS 498-007] Lecture 10. Training Neural Networks I (2) | 2024.01.29 |
|---|---|
| [EECS 498-007] Lecture 09. Hardware and Software (2) | 2024.01.25 |
| [EECS 498-007] Lecture 08. CNN Architectures (2) | 2024.01.24 |
| [EECS 498-007] Lecture 06. Backpropagation (1) | 2024.01.21 |
| [EECS 498-007] Lecture 04강 Optimization (1) | 2024.01.11 |