오늘은 4강 옵티마이제이션!
딱 2시 20분 시작인데 얼마나 걸리라나..
2번째 들을 때 적는건데 후다닥 끝났으면 좋겟슴니다
몬가 짱졸리고 꿀꿀한 날이야 🐽
후다닥 이번주가 지나갓으 ㅁ좋겟다
다들 행복해라.......
오늘의 주제인 최적화! Optimization은 loss를 최소화하는 W를 찾는 것으로
고지대에서 저지대로 갈 수 있는 길을 찾아 가는 것과 유사하다고 한다.

Linear Regression과 같은 모델에서는 미분을 통해 최소 loss를 가지는 W를 찾을 수 있지만,
복잡한 모델에서는 어떠한 수학적 공식을 통해 최적의 W를 찾는 것은 매우 쉽지 않은 일이다.
따라서 명시적인 수학적 공식을 통한 방법이 아닌 최소 loss를 가지는 이상적인 W에 맞게 조정해 나가는 방식을 사용하자!
먼저 첫번째로 소개된 방법은 Random Search 이다.
랜덤으로 선택된 W에 대해 훈련하고 성능을 평가하는데, 이를 반복하여 찾은 가장 낮은 loss값 일때의 W를 선택한다.
이는 탐색 공간이 클 경우 너무 오랜 시간이 걸리며 CIFAR 10 data 기준 기대 정확도가 95%인 반면,
15.5%로 좋지 않은 정확도를 가지고 있다. -> 너무 멍청한 알고리즘이야!
두번째 방법은 우리가 실제로 수행할 작업인 Follow the slope이다.
이는 기울기의 방향으로 항상 이동하여 최적화하는 방법을 말하며 간단하면서도 효과적이다.
loss function이 1차원이라면 걍 미분~ 해서 구할 수 있지만 다차원이라면 기울기는 각 차원의 편도함수로 이루어져 있다.
따라서 gradient를 이용해야 한다.
1) Numeric Gradiant
gradient를 구하는 첫번째 방법으로, 함수의 미분이 알려지지 않은 경우에 근사적으로 함수의 기울기를 계산하는 방법이다.
벡터 W에서 1개의 element씩 번갈아가며 각 element에 대응하는 gradient를 구하는 것이다.
유한 차분 근사에 의존해
특징
- 계산 횟수가 W의 크기에 비례하여 만약 W가 크다면 비효율적
- 속도가 너무 느려...
- h가 진짜 극한이 아닌 임의의 작은 수이기에 정확성이 떨어짐
- *h는 작은 변화량을 의미하며, 함수의 값을 조금 변화시켜 해당 위치의 기울기를 근사화하기 위해 사용
언제 사용할래!
- 함수의 미분이 직접적으로 필요하지 않을 때
- 미분을 계산하기 어려운 복잡한 함수 또는 머신러닝 알고리즘에서! -> 비선형 최적화 문제, CV?
2) Analytic Gradient
gradient를 구하기 위해 2번째로 소개된 방법이다. 이는 함수의 미분을 수학적으로 분석해 정확한 형태로 기울기를 계산하는데,
Numeric Gradiant의 단점을 보완했다고 볼 수 있다.
특징
- 정확성이 높고 빠른 계산속도
- 수치적 오류나 근사치의 문제를 고려하지 않아도 됨
- 복잡한 모델에서는 사용하기 어려움
언제 사용할래!
- 미분이 수학적으로 가능한 경우
- 정확한 gradient 계산이 필요한 경우
- 계산 비용이 낮고 수치적 오류를 피하고자 한 경우
위와 같은 두가지 방법을 비교해보자!
- Numeric gradient : 대략적이며 느리고 쓰기가 쉬워!
- Analytic gradient : 정확하고 빠르지만 오류가 발생하기 쉽다!
-> 결론은! 항상 Analytic gradient를 사용하되, Numeric gradient로 구현이 올바른지 확인하는 절차를 거치자!
수행할 때 실수가 없었는지 확인하는 디버깅 도구 방향으로 ~
위의 방법으로 gradient를 찾았다면 이제는 gradient를 활용하여 더 낮은 loss를 가지는 W를 찾아야 하는데,
Gradient Descent

그 방법을 Gradient Descent 라고 한다.
위 사진에서 x축과 y축은 가중치 행렬의 2차원 값을 표시하고 각 점의 색상은 목적함수의 높이를 나타낸다.
1. 흰색 점에서 시작하여 손실함수가 가장 많이 감소하는 방향인 음의 기울기를 계산한다.
2. 이 기울기 방향을 따라 작은 단계를 취하고
3. 내리막길을 반복적으로 반복한다.
경사 하강법은 3가지 Hyperparameter를 가진다.
- W(weight)를 초기화 하는 방법
- step 횟수 : 딥러닝에서는 보통 고정된 횟수를 사용
- Learning rate : 이동하는 거리, 값이 높으면 최적의 W까지 더 적은 횟수로 step도달이 가능하다. 하지만 W를 지나쳐버리는 overshoot의 문제가 생길 수 있으며 또 너무 낮으면 정교하지만 오래걸릴 수 있다.
- *overshoot : 목표값에 도달하기 전에 너무 많은 변화를 일으켜 최적화된 지점을 벗어나는 상황
경사하강법의 특징
- 아래쪽으로 바로 내려가지 않는다! -> 타코 그릇마냥 옆으로 돌아가.. 면서 목표 지점을 돌아다니는 듯한 움직임
- 처음에는 빠르게 진행되는 것을 알 수 있다.
- gradient 크기 (현재 위치에서의 기울기)가 커지면 더 큰 단계를 거치게 된다..
loss와 마찬가지로 gradient도 각 데이터의 합으로 이루어져 있다. 따라서 데이터가 많아질수록 gradient 계산에
많은 비용이 들기 마련이다(십만루프정도를 돈답니다). 따라서 SGD를 사용해보자!
Stochastic Gradient Descent

핵심 아이디어는 전체 데이터 셋이 아닌 무작위로 선택한 작은 배치 데이터를 사용하여 각 단계에서 모델을 업데이트 하자!
미니배치의 일반적인 크기는 32, 64, 종종 128 정도가 된다.
SGD에 필요한 Hyperparameter
기존 GD에서 사용된 것에 더해
4. batch size : mini batch의 크기 -> CPU가 허용하는 한, 최대한 크게 잡는 것이 좋당
5. data sampling : 데이터를 어떻게 선정할 것이냐! -> ranking 이나 prediction 등에선 중요할 수 있다
SGD에서는 표본 데이터를 가지고 gradient와 loss를 구하기에 표본 데이터의 분포가 전체 데이터의 분포와
최대한 유사하도록 표본을 선정해야 한다고 한다.
특징
- 빠른 업데이트 : 작은 배치를 사용하니까 ~
- 노이즈 감소 : 무작위성에 의한 노이즈가 존재하지만 이것이 최적화 과정을 일반화되게 만들어주는 효과가 있다.
- * 모델이 전체 데이터의 특이한 패턴에 과도하게 적응되는 것을 방지할 수 있답니다.
SGD의 문제점
1. Full Batch 보다 Overshoot 문제에 더 취약하다.

gradient descent가 지그재그를 그리며 진행되어 더 많은 step이 소요되기 때문.
최적점 주변을 번갈아 가면서 이동한다면 최적점을 지나쳐 움직이거나, 불안정하기 때문에!
-> 단계 크기를 작게 설정하면 방지할 수 있지만 ~ 매우 느려 ~ 그럼 또 목표에 도달 못 할지도!
-> 단계 크기를 크게 설정하면 최적점을 지나칠 수 있음!
즉, 한 방향으로는 빠르게, 다른 방향으로는 느리게 움직이는 상황에서 적절한 설정이 까다로워 진답니당 (고유 조건수가 높앙)
2. Local Minimum에 빠질 위험이 높다.

*local minimum : 함수 기울기가 0이지만 실제로 함수의 최하위는 아닌 함수의 지점.
로컬 미니멈에서 gradient를 사용하면 0이 되므로 단계 크기가 0으로 수렴되어 갇히게 되어버림..
또한 고차원 데이터에서는 Saddle point에 위치하게 될 수 도 있다. (고차원 최적화에선 일반적이야..)
*saddle point : 다변수 함수에서 어느 방향에서 보면 극대값이지만 다른 방향에서는 극소값이 되는 점.
-> 끝 부분 기울기가 0이기 때문에 gradient도 0이 되어 local minimum과 같은 맥락으로 갇히게 되는 것이다.
3. 확률적 부분 -> 노이즈가 많아!

전체 데이터 셋 중 일부 데이터로만 학습을 진행하기에 노이즈가 끼는 경우가 많아!
그래서 가고자하는 실제 방향과 잘 연관되지 않을 수 있다. -> 거꾸로 돌아가거나 애먼 곳으로 가는 등......
SGD + Momentum

그래서!! 순수 SGD만을 사용하기 보다는 약간 변형 시켜 Momentum이라는 친구를 추가해보려고 한다.
이 방법은 Linear 모델 말고도 다른 딥러닝 모델에서도 많이 쓰이고 있다.
여기서 Momentum은 관성이라고 이해하면 된다. 운동량의 개념이므로 속도와 방향이 존재하는데,
이전 단계의 움직임을 고려해 새로운 업데이트 방향을 결정하고, 이전 단계의 관성을 유지하면서 새로운 방향으로의 빠른! 이동을 돕는다.
특징
- local minimum, saddle point를 만나더라도 관성! 의 영향을 받아 쉽게 탈출 가능
- 지그재그로 움직이는 것을 방지해줌 -> 안정적이고 일정한 방향으로 빠르게 수렴하걸랑
- friction, decay rate와 같은 구체적인 하이퍼파라미터 존재
- -> 전 기울기 업데이트의 영향을 얼마나 반영할 지 제어하는 역할 즉, momentum의 효과를 얼마나 유지할래 ~
- 낮게 설정 -> 이전 기울기 영향 줆 -> 관성 작아짐 -> 많은 새로운 정보 반영
- 높게 설정 -> 이전 기울기 영향 커짐 -> 관성 커짐 -> 이전 정보 반영
- 일반적으로 0 - 1 사이의 값으로 설정, 보통 0.9!
Nesterov Momentum

지난 step 정보를 반영하는 것이 아닌!
현재 위치에서 velocity 만큼 이동했을 때의 gradient를 이용해서 step을 정하는 Nesterov Momentum 방식이 있다.
현재 위치에서의 모멘텀을 사용하여 미래 위치에서의 gradient를 예측하고, 이를 기반으로 매개변수를 업데이트 한다.
즉, 조금 앞선 gradient!
특징
- 기존 Momentum Optimizer 보다 더 빠른 수렴 속도 제공
- 미래 위치를 고려하기에 보다 정확한 방향으로 수렴할 가능성이 높음
- 고차원이나 복잡한 모델에서의 성능이 향상되는 경향
한계점
- SGD + M 에 비하여 local minimum에 더 잘 빠질 수 있다. 시원시원 과감하게 내려가기 보다는 약간 간보면서 방향을 결정하는 경향이 있으므로 local minimum에 빠질 가능성이 더 크다고 생각한다.
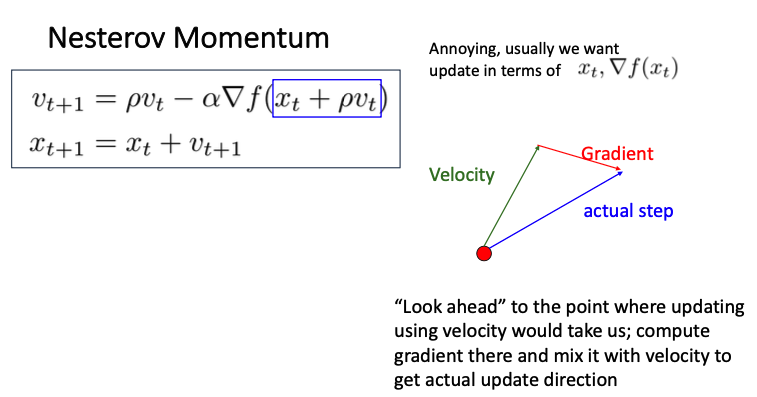
위와 같은 방식으로 구하는데, 이 방식은 api등을 적용하기 어렵다는 한계가 있다.
여기서는 속도가 기울기의 반대 방향을 가리키도록 만들고, 학습률 알파를 속도 벡터와 함께 반영하는 것이다.

그래서 위와 같이 살짝 변형하여 적용해 본다.
AdaGrad

adaptive learning late를 활용한 AdaGrad라는 방법도 있다.
- gradient 큰 경우 -> 큰 값으로 나눔 -> step size 작아짐
- gradient 작을 경우 -> 작은 값으로 나눔 -> step size 커짐
- 따라서 GD의 진행이 지그재그를 이루는 Poor Conditioning 을 완화시킬 수 있다.
- 하지만, step이 많이 진행될수록 grad_squared가 커져서 gd 그냥 멈춰버리는 조기중단 사태가 발생할 수 있다.
분모가 너무 커져서 학습률이 작아져 gradient descent가 빨리 멈출 수 있는 점을 개선해보자!

RMSProp
gradient 제곱의 지수 이동 평균을 사용하여 누적값이 증가하는 것을 방지한다.
step size는 점점 줄어드니까 SGD + Momentum에 비해 overshoot이 덜 하다는 특징이 있다.
Adam : RMSProp + Mometum

Adam에서 하이퍼파라미터는 beta1과 beta2가 추가로 존재한다.
코드를 보면 beta2는 1에 가까울 수록 t = 0에서 step size가 매우 커지게 된다. 따라서 너무 큰 수가 되는 것을 방지하기 위해서
bias correction을 추가한다.


Adam의 주요 특징들을 정리해보자!
사실 위에 나왔던 다양한 알고리즘을 합친(?) 느낌이라 같은 이야기의 반복일 수 있다는 점 주의해야한다 ㅎㅎ
먼저 적응적 학습률을 사용한다는 점이다. Adagrad의 특징을 가지고 있기때문에 각 매개변수에 대해 개별적인 학습률을 조정함으로써
수렴을 더 빠르게 만들 수 있다.
두번째로는 모멘텀 기법이다. 지난 gradient의 지수 평균을 사용하여 모멘텀을 적용한다.
마지막으로 bias correction이다. 학습 초기에 편향이 발생하는 것을 보정하기 위해 사용한다. 더욱 안정적일 걸 !
Adam은 다양한 딥러닝에서 robust하게 사용된다. 특히 대규모 데이터 셋이나 복잡한 모델이서 빠른 수렴을 제공하는 장점이 있어
많이 쓰이고 있다.
하지만 항상 Adam이 최고야 ~ 라는 자세는 좋지 않다.
optimizaition 역시 하이퍼파라미터 적인 성향(?)으로 다가가야 한다. 데이터셋, 모델의 구체적인 상황에 따라 최적의 최적화 방법은 항상 다르다는 것을 알고! 실험적인 자세로 최적화에 다가가야 한다구 생각한다.

위에서 주섬주섬 끄적였던 말들을 표로 정리해주었다.
복습 느낌으로 다시 하나하나 이해하면서 보면 좋을 듯 하다.
지금까지 배운 Optimization응 모두 1차 미분만을 이용한 Fist-Order Optimization 이다.

하지만 당연히 Second-Order Optimization 도 존재한다.
2차 최적화는 2차 도함수(헤시안 행렬)를 사용하여 최적화하는 방법을 말한다. 두번째 도함수 정보를 추가로 활용하여
보다 정교하고 빠른 수렴을 이루려 한다.
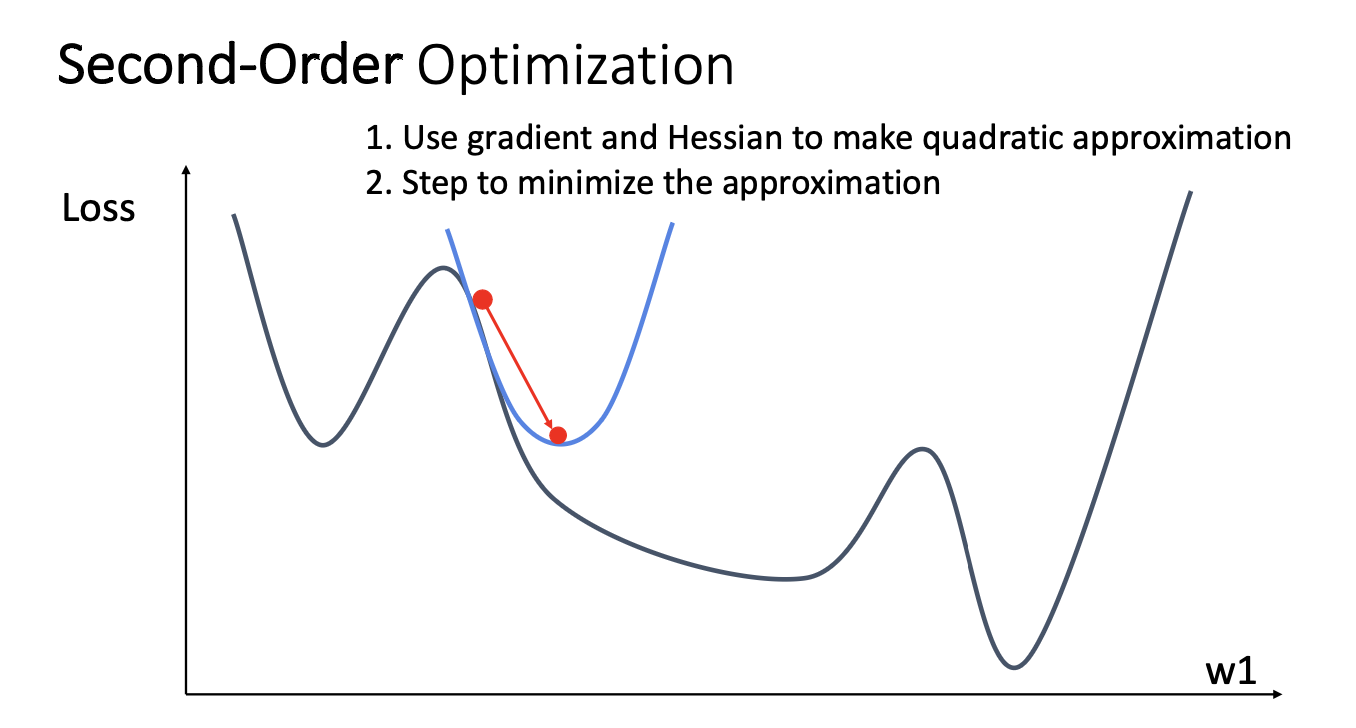
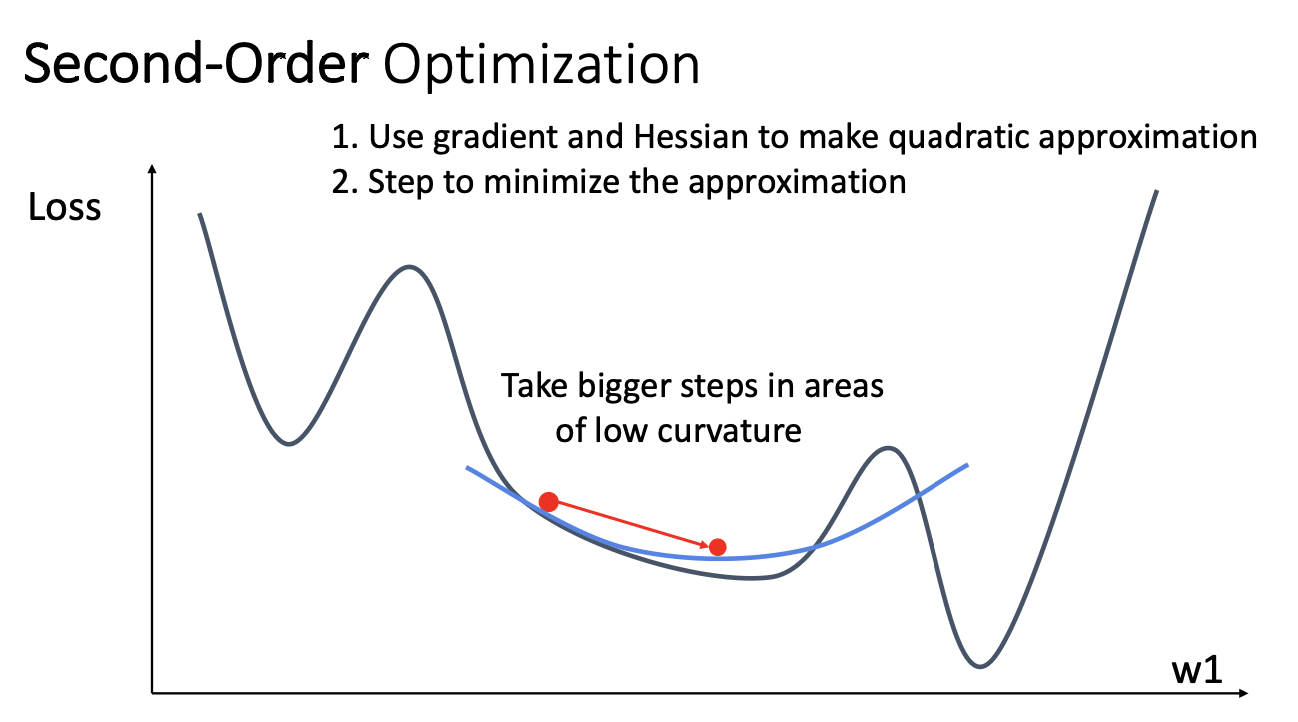
이 방식은 loss의 곡률과 step size가 반비례하기에 First-Order 보다 더 robust한 최적화 방식이라 볼 수 있다.
근데 해시안 행렬의 역행렬을 계산해야 하기 때문에 계산 비용이 높을 수 있다. 특히 딥러닝에서는 매개변수가 많고 복잡하기에
역행렬 계산이 매우 비실용적일 수 있다.
따라서 실제로는 뉴턴 메소드의 변형이나 2차 최적화의 다른 형태를 사용하기도 한다.
예를들면 L-BFGS!
L-BFGS
큰 데이터 셋이나 매개변수 공간이 큰 문제에서도 효과적으로 사용할 수 있는 친구!
핵심 아이디어는 최근 업데이트된 일부 gradient 정보를 기억하고, 이를 사용하여 헤시안 행렬의 근사값을 계산하는 것이다..
메모량 사용이 적고 효과적인 수렴을 제공하는 장점이 있답니다 ~
이번 강의는 Optimization ! 이었다.
loss를 최소화 하는 가중치 행렬 W를 찾기 위해 사용했답니당.
드디어 다 쓴(이틀 뒤임) 이번 블로그.
진짜 애먹었다
사실 뒤로 갈수록 진빠졌어
티날라나
흐린눈 해주기~
험난한 스터디를 헤쳐나가는 이번주 였슴니다
그래두 주말에 여행가니까 ~ 열심히 놀라믄 공부해야징
부족한 점 짱많은 포스팅이야
귀엽게 봐주세요 뿌잉
......
이런 거 하지말까?
'EECS 498-007' 카테고리의 다른 글
| [EECS 498-007] Lecture 10. Training Neural Networks I (2) | 2024.01.29 |
|---|---|
| [EECS 498-007] Lecture 09. Hardware and Software (2) | 2024.01.25 |
| [EECS 498-007] Lecture 08. CNN Architectures (2) | 2024.01.24 |
| [EECS 498-007] Lecture 06. Backpropagation (1) | 2024.01.21 |
| [EECS 498-007] Lecture 03강 Linear Classifier (2) | 2024.01.08 |