아 십..
진심으로 화나는 순간이야
3일동안 열~ 심히 이번 강의를 쓰구있엇어
진짜 강의 10분 남았는데
거의 다 썻는데
무슨 줄주리 쏘시지마냥 짱 길었는데
와이파이 이슈로 그냥 뿅! 하고 사라졌어....
처음부터 다시 쓰는 이 마음 알아?
발표강의라서 열심히 했는데...
그럼에도 해야지 어쩌겠어..
에도 한계가 있다 .
저번 시간 강의에서 마지막에 던진 물음표가 있었다.
실제로 gradient를 어떻게 계산할래? 기울기 어떻게 계산할래?
이번 강의에서는 gradient를 구하는 방법! 이 핵심이 될 것이다.
첫번째로 단순하게 제시한 방법은
1) 손으로 구해보기! 종이에 구해보기!
하면 함 이겠지...

하지만 이것은 많은 문제점을 가지고 있다.
먼저 매우 많은 연산량을 포함하고 있다.. 많은 종이가 필요하겠고.. 많은 시간이 필요하겠지!
또한 모듈화가 되어있지 않다. 내가 softmax를 쓰다가 SVM으로 바꾸면? 처음부터 다시 계산해야해!
(마치 나같다.. 첨부터 다시 쓰는..)
그래서 아마 곧 포기에 이를 것 같은 이 방법은 좋은 방식이 아니다.
그렇다면!
2) Computational Graph

computational graph는 우리 모델 안에서 이루어지는 연산들을 그래프의 형태로 나타낸 것이다.
파란색 노드는 input x와 w의 곱, 빨간색 노드는 loss, 초록색 노드는 regularization term을 더하는 형태로 최종 L를 구한다.
위의 computational graph는 linear classifier를 나타낸 형식적인 그래프이다. 하지만 모델이 점점 더 커지고 복잡한 형태가 될수록
이러한 구조화된 그래프는 매우 중요하게 다가올 것이다.

AlexNet의 경우 deep network로 많은 layer를 통해 계산이 진행될 것이다 .
또한 Neural truring machine은


엄청 크고 복잡한 computational graph로 되어있는 것을 볼 수가 있다.
더하여 반복네트워크라 여러 시간단계에 걸쳐서 전개되는데 이를 다 손으로 계산할 수는 없을 것이다.
그래서! computational graph를 사용하자!
computational graph를 활용한 backpropagation 과정을 간단한 예제를 통해 알아보자!
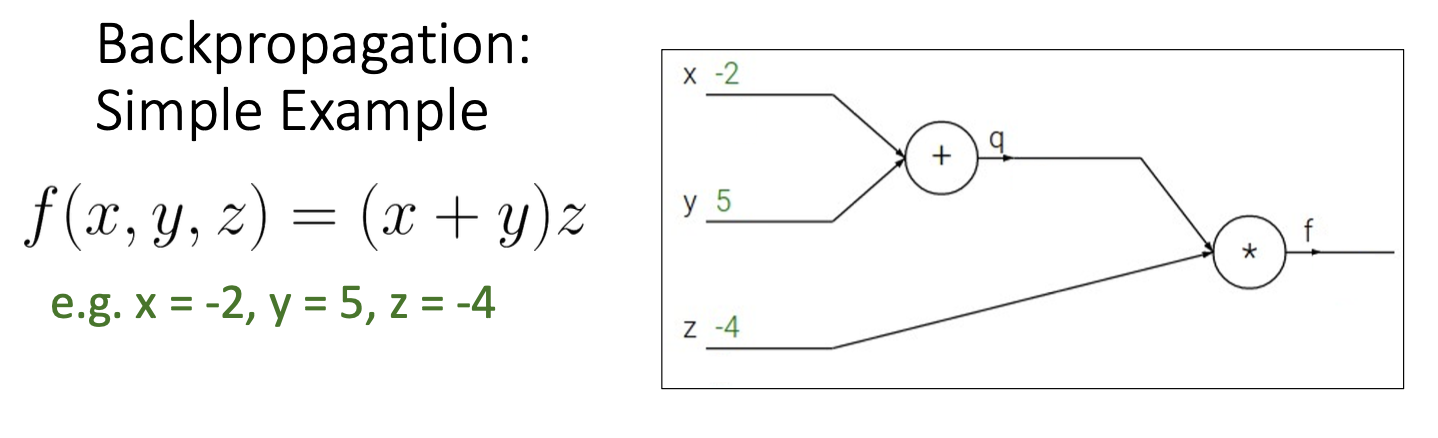
input x, y, z가 이렇게 주어졌을 때,

1) forward pass를 통해 output을 계산하자.
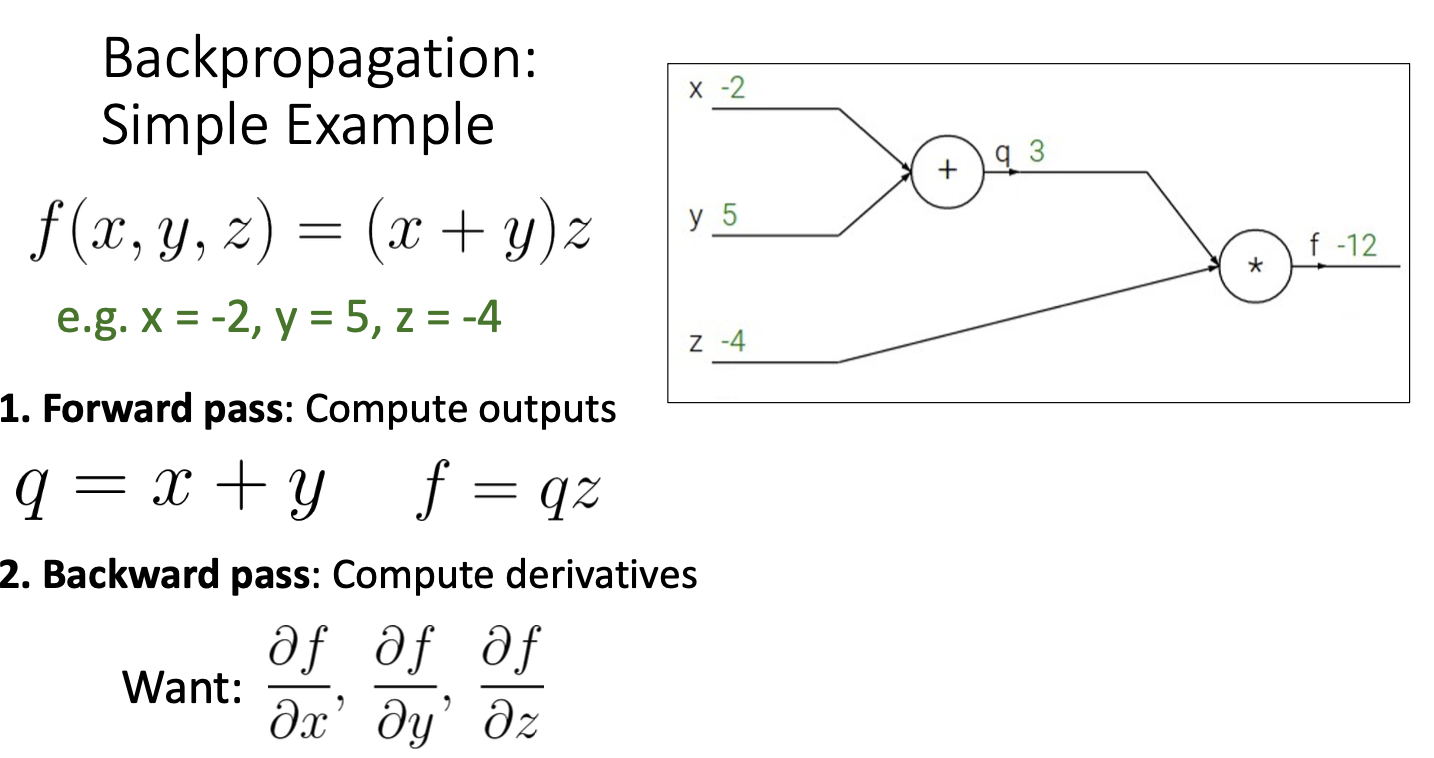
2) backward pass 를 통하여 gradient를 계산하면 된다.
output쪽 노드부터 전체 function인 f를 각 노드가 나타내는 함수로 편미분하여 upstream gradient를 구하고,
chain rule을 적용시켜 local gradient(현재 노드에 대한 gradient)를 upstream gradient와 곱해주어 상위 노드인 downstream gradient를 계산해준다.
여기서 f에 대한 gradient는 자기 자신에 대해 미분한 값으로 1이 된다.
2-1) local gradient 계산하기

local gradient는 현재 노드에서의 gradient라고 할 수 있다.
chain rule을 통해 수식을 풀어 local gradient를 구하여준다.
2-2) downstream gradient 계산하기
위 사진처럼 downstream gradient는 local gradient와 upstream gradient의 곱으로 구할 수 있다.
한 노드의 관점에서 바라본다면

위 사진처럼 나타내볼 수 있다.
upstream gradient가 흐르면 local gradient를 구해서 곱한 후 downstream gradient를 구하여준다.
구한 그 downstream gradient는 또 다른 노드의 upstream gradient가 되어 흐르는 것이다.
다른 예제를 살펴보자!

위는 input이 5개인 경우이다.
w0와 x0의 곱과 w1와 x1의 곱을 더한 후, w2를 bias항으로 더하여 sigmoid함수를 씌워주는 computational graph를 나타낸다.

앞서 봤던 예제처럼 먼저 foward pass를 통해 최종 output을 계산하여 준다.
다음

backward pass를 통해 gradient를 구하여준다.
예시 하나만 보자면

현재 upstream gradient는 1이고, local gradient를 구해야한다.
1/x 노드이므로 이를 x에 대해서 편미분해주면 -1/x^2의 형태가 되며 현재 x인 1.37을 대입하여 준다.
대입 결과는 -0.53이 되며 upstream gradient인 1을 곱하면 downstream gradient는 -0.53이 된다.
같은 방식으로 나머지 노드들도 계산을 진행해주면 된다.
여기서 주목해야할 점이 있는데,
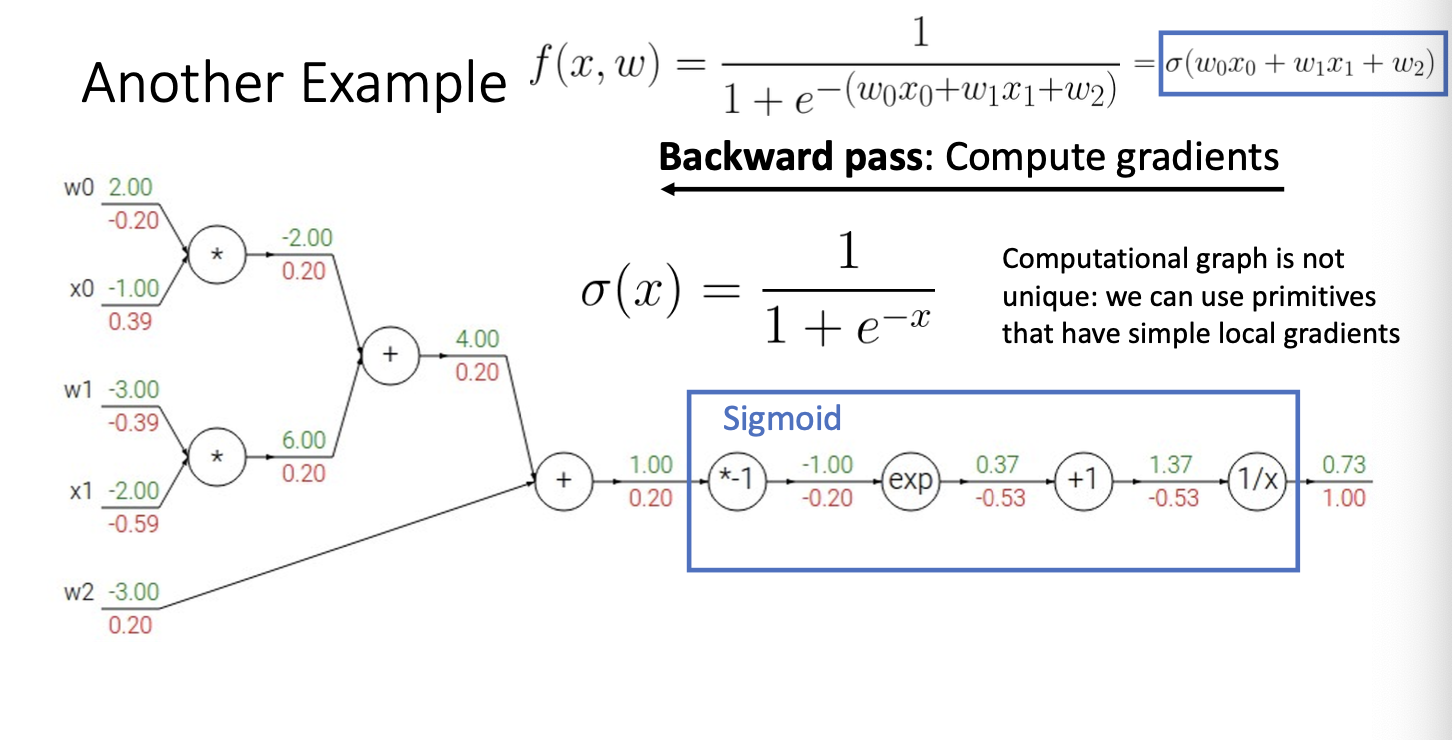
여기서 위 파란색 박스 안에 있는 4개의 노드는 sigmoid 함수를 나타내고 있다.
이를 하나로 보고 delta(x)로 치환을 해보자! 하나로 생각하자!

다음 위 식을 미분해주면 위와 같은 결과를 얻을 수 있다.
이를 이용하여 다시 downstream gradient를 구해보자 .
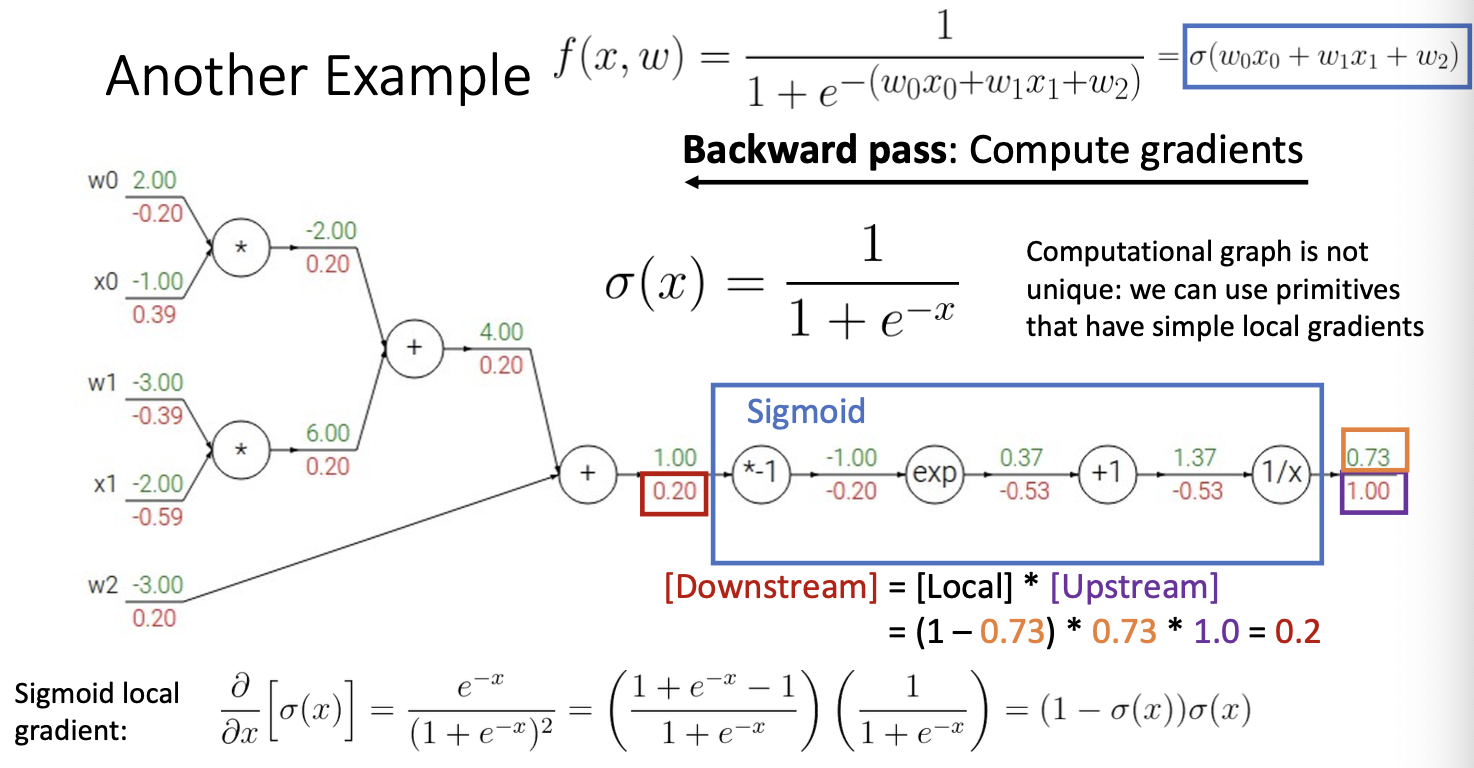
구해진 미분 식에 0.73을 대입한 후 upstream gradient인 1을 곱하여주면 나타난 것과 같이 0.2의 downstream gradient가 계산되는 것을 볼 수 있다.
따라서 computational graph는 중간과정을 생략하고 표현할 수 있다는 특징이 있다.
위에서 계속 예제를 보면서 눈치를 챘을수도 있었던! gradient 흐름의 흥미로운 패턴이 존재한다.

- add gate : gradient distributor -> 그대로 흘려줌
- mul gate : swap multiplier -> 상대방 value x upstream gradeint
- copy gate : gradient adder -> input의 변화가 여러군데 영향을 끼칠때!
- max gate : gradient router -> max 값에만 흐르게하기, 너무 남발(?)하면 0이되는 gradeint가 많아져서 빠르게 중단될 수도 있어
이러한 backpropagation을
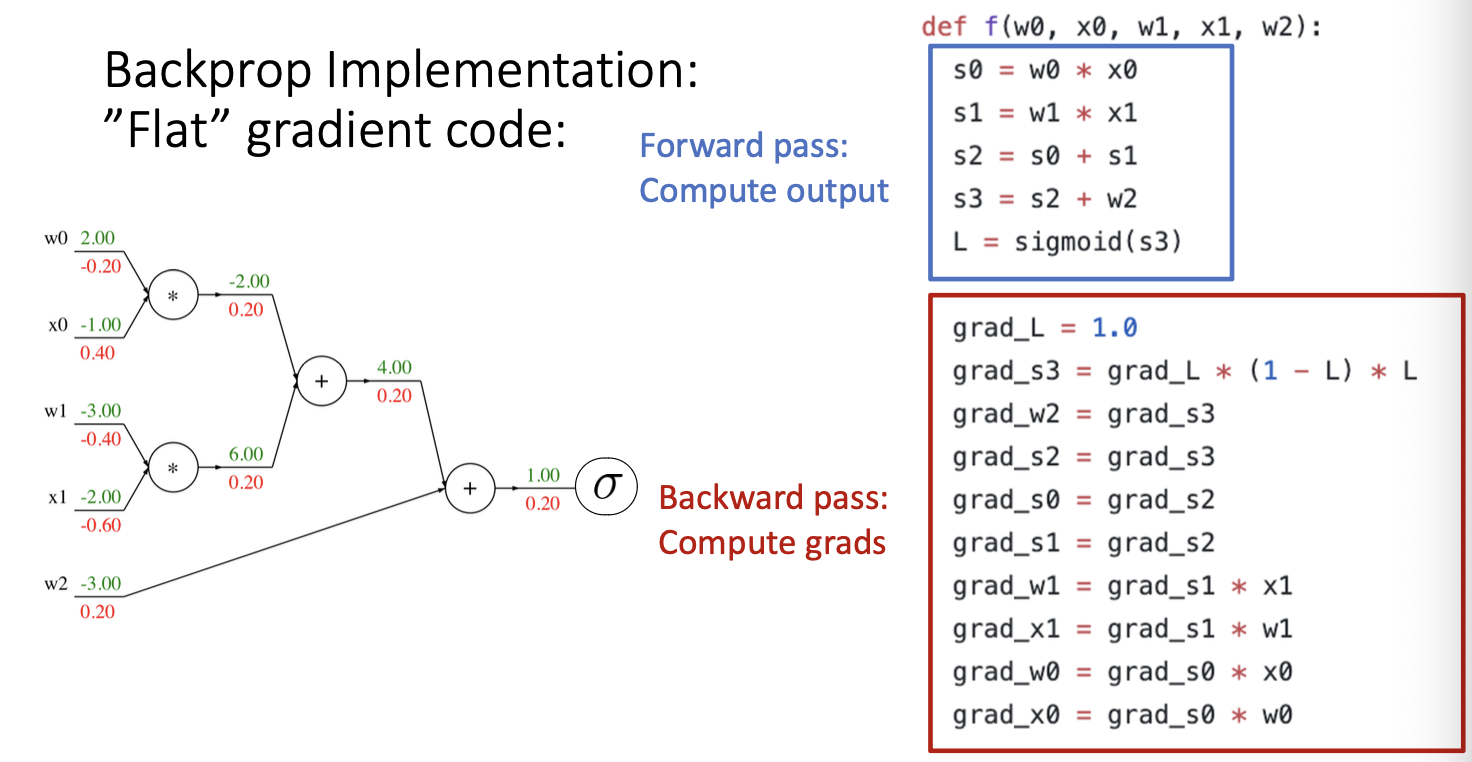
위와 같은 코드로 간단하게 구현해볼 수 있다.
또한 모듈화된 형태로도 사용할 수 있는데,

위의 foward 함수에서 보면
self.graph.nodes_topologically_sorted()라는 함수에서 forward 과정에서 수행되는 연산들을 순서대로!
무엇을 먼저 연산해야하는지 sorting하는 과정을 거친다.
다음 backward 함수를 보면
위의 sort를 reverse하여 제일 뒤에 있는 것부터 backprop과정을 하도록 구현해놓은 것을 볼 수 있다.
pytorch 에서는

위와 같이 구현이 되어있다.
우리가 앞서 언급했던 패턴에 의해 gradient를 빠르게 구하려면 forward과정에서 구했던 현재 그 노드들의 값을 알아야했다.
따라서 forward 함수에서 보면 ctx.save_for_backward(x, y)를 통해 현재 x, y값을 tensor 형태로 저장하여
backward 함수에서 저장된 tensor를 불러와 gradient를 계산하고 있는 것을 볼 수 있다.

더하여 위와 같이 pytoch에서는 c++의 형태로 sigmoid 함수를 정의하고 있다.

우리는 지금까지 모두의 값이 scalar인 경우만 살펴보았다.
하지만 현실에서는 그런 경우보다 vector 형태인 경우가 다수일 것이다.
그렇다면 vector 값이라면 어떨찌! 살펴봐야겟찌
그 전에 먼저 미분에 대한 3가지 형태를 알아보도록 하자!
1. input, output이 모두 scalar인 경우

위와 같은 경우에는 미분 값도 scalar로 도출된다. 우리가 앞서 보았던 모든 경우가 이에 해당한다.
2. input : vector, output : scalar인 경우

위와 같은 경우에는 미분 값 형태가 vector가 된다. input의 차원 수와 같은 차원으로 도출되며 gradient가 된다.
gradient의 n번째 element가 n번째 input이 조금 변화했을 때, 전체 output이 얼마나 변하는지를 나타내는 것이다.
3. input, output 모두 vector인 경우

위와 같은 경우, 미분 값의 형태는 matrix가 된다. 1차 도함수의 경우이므로 jacobian matrix이다.
jacobian의 n번째 input이 변화할 때, m번째 output의 변화 정도를 의미한다.
input과 output이 vector인 경우를 한 노드의 관점에서 바라보아 보자.
여전히 loss는 scalar인 점 알아두자!

- upstream gradient를 보면, scalar인 loss를 vector인 z로 편미분하고 있다. 따라서 upstream gradient는 위에서 본 2번째 경우에 해당하므로 z차원의 vector가 될 것이다. -> z vector의 각 요소가 loss에 얼마나 영향을 미칠까!
- x에 대한 local gradient만 보면, vector인 x, z로 편미분을 하고 있다. 따라서 local gradient는 위에서 본 3번째 경우에 해당하므로 x x z matrix 형태의 jacobian matrix가 된다.
- downstream gradient는 chain rule을 통해 upstream gradient와 local gradient를 곱해주고 있다. matrix x vector의 값은 vector 형태 이므로 vector가 된다.
다음 Relu function을 적용한 vector backprop에 대해서 살펴보장

우리의 input vector x가 위와 같이 주어졌을때, relu func을 통과하면 다음과 같은 output vector를 만날 수 있다.
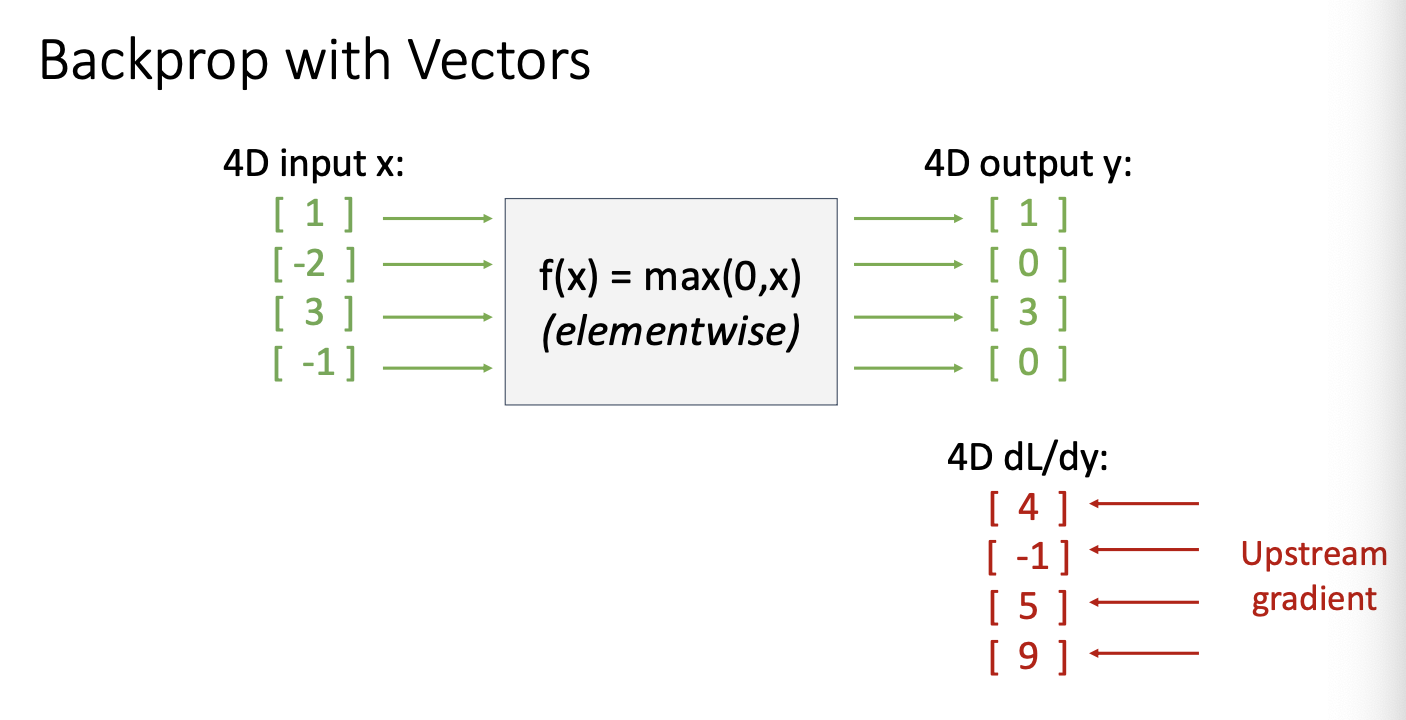
여기서 우리의 upstream gradient가 다음과 같이 주어졌을 때,

local gradient를 x에 대한 y의 편미분 형태로 구한 후 (jacobian matrix) upstream gradient를 곱하여주면
위와 같은 형태의 downstream gradient를 얻을 수 있다.

하지만.. 여기서 실제로 사용되는 vector들은 고차원 미분이 진행되기에 jacobian matrix는 매우 커져 연산량이 증가하게 될 것이다.
또한 matrix 값들의 대부분이 0이 되는, sparse해지는 희소행렬의 형태가 될 것이다.
희소행렬의 형태가 된다면 함수의 출력이 입력의 일부에만 의존하게 되며 메모리의 사용이 많아질 것이다. 더하여 연산량 측면에서 비효율적이며 속도도 느려질 것이다.
그래서 jacobian matirx를 명시적으로, 직접적으로 딱! 사용하지 않고 암시적인, 수치적인 형태로 접근하여 계산에 이용해보자

위와 같이 element 하나의 관점에서 바라보며 부호를 비교하고, upstream gradient를 흘려주는 동작과정을 볼 수 있다.
이제는 input과 output이 vector가 아닌 matrix 형태일 때 backpropagation을 살펴보자

위와 같은 방법이지만 x, y, z가 모두 vector가 아닌 matrix라고 생각하면 된다.
구체적인 예시를 보자.

각 input과 output에 대하여 살펴보장
일단 input x는 N by D 형태의 행렬이다. D차원의 vector N개를 가지고 있는 형태의 행렬이라고 볼 수 있는데,
주어진 행렬로 보자면 3차원 벡터 2개를 가지고 있다.
다음 input w도 마찬가지이지만 transpose시킨 형태로 D차원의 vector M개를 가지고 있는 형태의 행렬로,
주어진 행렬로 보면 3차원 벡터 4개를 가지고 있다.
마지막으로 output y는 matrix multiplication 형태로 각 element가 x와 w의 element로 이루어진 선형결합의 형태이다.
예를들어 y11 = x11 * w11 + x12 * w21 + x13 * w13 이다.
이제 backpropagation을 통해 x의 gradient를 구하자.

앞서 계속 말했듯 downstream gradient는 local gradient와 upstream gradient의 곱으로 나타낼 수 있다.
upstream gradient는 scalar인 Loss를 matrix인 y로 미분해 주었기에 N by M 형태의 matrix로 나타난다.

또한 local gradient는 위와 같은 형태(dy / dx, dy / dw)의 매우 큰 Jacobian matrix가 된다.
이는 vector에 대한 Jacobian보다 훨씬 더 큰 형태이므로 더욱 더 감당하기 힘들 것이다.
따라서 우리는 jacobian matirx 전체를 multiplication 하여 downstream gradient를 구하는 것이 아닌,
jacoblian matrix를 암시적으로 사용하여 요소 하나 하나의 관점에서 값을 구해보는 방향으로 접근해야 한다.

일단 w가 아닌 x에 대한 downstream gradient에 대해 먼저 살펴보자. 이는 Loss가 스칼라 값이므로 당연하게 x의 형태와 똑같다.
이런 dL / dx에서 첫번째 element(파란색 상자)를 구해보면,
L을 x전체가 아닌 하나의 element로 미분해주면 된다. 이에 chain rule을 적용시키면

이와 같은 식을 세울 수 있고, 빨간색에 해당하는 upstream gradient는 주어졌으므로 주황색에 해당하는 local gradient를 구해야한다.
또한 위 식에서 볼 수 있듯 언제나, 항상! downstream = local x upstream !

주황색 local gradient를 구하기 위해서는 또 각각의 element 관점에서 바라보아야 한다.
첫번째 요소(보라색 글씨)를 먼저 보자면, 아래(검정색 글씨)와 같은 수식으로 나타낼 수 있다.
정리하면 dy11 / dx11 을 ㄹ구하기 위해 y11을 살펴보면 위에서 언급했던 선형 결합의 형태로 나타내진다.

이 y11을 x11로 편미분하면 위의 선형 결합 형태에서 상수항은 날라가고 w11만 남게되어 주어진 행렬에서 계산하면 3이 될 것이다.
위와 같은 방식으로 local gradient를 element관점에서 하나하나 구하다 보면! 규칙을 발견할 수 있을 것이다.

위 사진에서 확인할 수 있듯, local gradient의 첫번째 행이 w의 첫번째 행과 같다는 점을 볼 수 있다.
그렇다면 두번째 행은! 어떻게 될까?

두번째 행은 모두 0가 된다. 이는 사실 매우 당연한 현상이다!
y12의 element관점에서 생각해보자면, y12를 x11로 편미분 한 것이므로 y12의 선형결합 형태에서 x11은 전혀 관여하지 않았기 때문에
x11항은 존재하지 않으며 편미분을 진행할 경우 모든 항이 상수처리 되어 없어지게 된다.
그렇다면 x에 대한 local gradient를 모두 구했다!
이제 upstream gradient와 곱하여 downstream gradient를 구하면 된다.
연산해주면 최종적으로 dL / dx11 의 downstream gradient의 값은 0이 되고,
모든 요소에 대하여 위와 같은 연산들을 해주면 최종적으로 아래와 같은 downstream gradient를 구하게 된다.
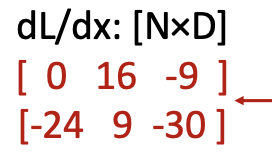
여기서 흥미로운 점을 발견할 수 있다.
element 하나의 관점에서 바라보니 행렬 관점에서 규칙을 발견할 수 있었다.
아래 그림과 같이 두 matrix의 순서를 바꾸고 upstream gradient를 transpose 취해주면 한 번에 downstream gradient를 구할 수 있다. dw도 역시 같은 맥락으로 아래 두번째 식이 성립하게 된다.

Backpropagation의 또 다른 관점을 보자.

위 경우는 input이 vector, output이 scalar인 경우를 나태내고 있다.
이 경우에는 나머지 local gradient는 모두 matrix의 형태지만 마지막은 x3 shape과 같은 D3임을 알 수 있다.
우리는 matrix x matrix 형태를 피하는 것이 좋으므로 뒤에서부터! 오른쪽에서 왼쪽으로 연산을 하는 것이 이득임을 알 수 있다.
따라서 D3부터 연산을 진행하면 matrix x vector 의 형태이므로 vector가 나올 것이다.
그렇다면 반대로 input이 scalar이고 output이 vector인 경우에는 어떻게 gradient를 구하는 것이 좋을까?
Foward-mode로 진행하는 것이다.

left-to-right 즉, 왼쪽에서 오른쪽으로 진행하는 것이 matrix x matrix 연산을 피할 수 있을 것이다.

하지만 이 경우는 안타깝게도(?) pytorch나 tensoflow에는 구현되어있지 않다고 한다.
Automatic Differentiation은 계산의 효율성에 관한 알고리즘이다.
forward mode와 reversse mode는 사실 계산의 결과는 같다. 하지만 주어진 모델의 형태의 따라 어떤 방식으로 진행할 지에 따라
계산의 효율성이 달라지는 것이다.
또 다른 경우를 생각해보자.
지금까지는 1차 미분에 대해서만 생각했다. 하지만 고차원 미분이라면! 히히
2차 미분이라고 예를 들자면,

위와 같은 우리의 모델이 있고, loss를 x에 대해서 2번 미분한 Hessian 행렬이 있다.
하지만 이 행렬에 어떠한 vector를 곱하는 것 보다

위와 같이 jacobian x vector의 형태로 표현하여 계산할 수도 있다. 이는 계산의 효율성과 수치적 안정성 등을 생각했을 때
보다 효율적이고 좋은 연산 방법이다.
그리고 이러한 Hessian matrix를 또 다른 방식으로도 구할 수 있다.

위의 분홍색 밑줄이 쳐진 부분을 얻기 위해 일종의 backpropagation을 진행한다.

그 다음 위와 같은 computational graph가 생성되었을 때, 전체과정을 backprop을 적용하면 Hessian matrix를 얻을 수 있다고 한다.
그런데 왜 굳이.. 이렇게? 라는 생각이 들었다..
이러한 과정을 통해 Hessian matrix를 얻는 이유! 에 대해 생각해 보았는데, (정답인진 몰라 냎ㅎ피셜)
저저번 시간 4강 optimaization 에서

이 슬라이드를 본 적이 있을 것이다!
여기서 hessian matrix는 비실용적! N이 너무 커져서 시간 복잡도가 증가한다는 점을 잠시 언급했었다.
이러한 맥락에서 hessian matrix를 그대로 연산에 이용하거나 바로 구하려고 하는 경우 많은 메모리와 연산량을 요구할 것이다.
따라서 backprop의 과정을 거쳐 hessian matrix를 얻어 계산에 활용하려는 것이 아닌가! 싶었다.
사실 2차 미분에서는 크게 와닿지 않을 수 있다고 생각한다.
2차가 아닌 훨씬 고차원 미분이 진행될 경우 hessian matrix는 엄청나게 커질 것이다.
이를 연산에 이용하기엔 더욱 벅찰테니! computational graph를 확장하여 backpropagation을 통해 보다 쉽게 구할 수 있을 것 같다.
휴 길고 길었던 이번 강의를 요약하자면,


gradient를 구할 때, 손으로 직접하지말고! computational graph를 사용하여
다음 forward pass 를 통하여 output, 즉 우리의 loss를 구하고!
다시 backward pass를 통해 gradient를 구하자 였다...
backward 연산을 진행할 때, downstream gradient는 upstream gradient와 local gradient의 곱으로 구할 수 있었으며,
이를 python 코드로 간단히 나타낼 수 있었다.
더하여 모듈화된 방식을 사용하여 더욱 간단히 나타내어 볼 수 있었다!
끝!
다음 이시간에...
아 진짜 우역곡절 가득한 포스팅 이었다
소중하게 써왔던 글들을 다시 쓰려니 추가된 부분도 있찌만
뺴먹은 부분도 있을 것 같아 마냥 슬푸다
발표까지 진행했던 부분이라
backpropagation은 그냥 이제 easy~ 히히
새벽 두시다 집이나 가자 윤히야
고생해따
'EECS 498-007' 카테고리의 다른 글
| [EECS 498-007] Lecture 10. Training Neural Networks I (2) | 2024.01.29 |
|---|---|
| [EECS 498-007] Lecture 09. Hardware and Software (2) | 2024.01.25 |
| [EECS 498-007] Lecture 08. CNN Architectures (2) | 2024.01.24 |
| [EECS 498-007] Lecture 04강 Optimization (1) | 2024.01.11 |
| [EECS 498-007] Lecture 03강 Linear Classifier (2) | 2024.01.08 |